Гармонический закон колебаний в контуре

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса.

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки. (рис. 1

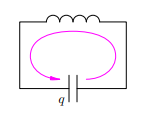
Рис.1. Положительное направление обхода

Сила тока считается положительной (I > 0), если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной (I < 0).

Заряд конденсатора q — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае q — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: q˙ = I (при ином выборе знаков могло случиться q˙ = −I). Действительно, знаки обеих частей совпадают: если I > 0, то заряд q левой пластины возрастает, и потому q˙ > 0.

Величины q = q(t) и I = I(t) меняются со временем, но энергия контура остаётся неизменной:

Стало быть, производная энергии по времени обращается в нуль: W˙ = 0. Берём производную по времени от обеих частей соотношения (3.92); не забываем, что слева дифференцируются сложные функции:

Подставляя сюда q˙ = I и I ˙ = q˙˙, получим:

Но сила тока не является функцией, тождественно равной нулю; поэтому

Перепишем это в виде:

Мы получили дифференциальное уравнение гармонических колебаний вида , где. Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т. е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

Циклическая частота ω0 находится по формуле (2); амплитуда q0 и начальная фаза α определяются из начальных условий

Мы рассмотрим ситуацию, подробно изученную в начале. Пусть при t = 0 заряд конденсатора максимален и равен q0; ток в контуре отсутствует. Тогда начальная фаза α = 0, так что заряд меняется по закону косинуса с амплитудой q0:

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (4), опять-таки не забывая о правиле нахождения производной сложной функции:

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

Амплитуда силы тока равна:

Наличие «минуса» в законе изменения тока (5) понять не сложно. Возьмём, к примеру, интервал времени 0 < t < T/4.

Ток течёт в отрицательном направлении: I < 0. Поскольку ω0 = 2π/T, фаза колебаний находится в первой четверти: 0 < ω0t < π/2. Синус в первой четверти положителен; стало быть, синус в (5) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (5).

Изобразим графики колебаний заряда и тока, т. е. графики функций (4) и (5). Для наглядности представим эти графики в одних координатных осях (рис. 2).

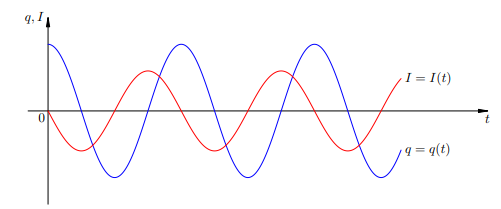
Рис.2. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

Запишем закон изменения тока (5) в виде:

Сопоставляя это выражение с законом изменения заряда q = q0 cos ω0t, мы видим, что фаза тока, равная ω0t + π/2, больше фазы заряда ω0t на величину π/2. В таком случае говорят, что ток опережает по фазе заряд на π/2; или сдвиг фаз между током и зарядом равен π/2; или разность фаз между током и зарядом равна π/2.

Опережение током заряда по фазе на π/2 графически проявляется в том, что график тока сдвинут влево на π/2 относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз π/2).

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 3).

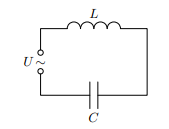
Рис. 3. Вынужденные колебания

Если напряжение источника меняется по закону:

то в контуре происходят колебания заряда и тока с циклической частотой ω (и с периодом, соответственно, T = 2π/ω). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте ω0 = 1/ √ LC.

Амплитуда вынужденных колебаний заряда и тока зависит от частоты ω: амплитуда тем больше, чем ближе ω к собственной частоте контура ω0. При ω = ω0 наступает резонанс.