Колебательный контур с резистором

Колебательный контур с резистором

Рассмотрим вынужденные колебания, происходящие в колебательном контуре с активным сопротивлением. К источнику переменного напряжения U последовательно подключены: резистор сопротивлением R, катушка индуктивности L и конденсатор ёмкости C (рис. 1; такой контур называется ещё RLC-контуром).

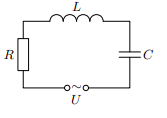
Рис.1. Колебательный контур с резистором

Так как элементы соединены последовательно, сила тока в них одинакова в любой момент времени (вспомните условие квазистационарности!). Поэтому нам будет удобно начать не с напряжения источника, как раньше, а с силы тока, и считать, что ток в цепи колеблется по закону синуса:

1. Пусть UR — мгновенное значение напряжения на резисторе. Оно связано с силой тока обычным законом Ома:

2. Напряжение на конденсаторе UC отстаёт по фазе от тока на π/2; это значит, что фаза напряжения UC равна ωt − π/2. Амплитуда напряжения UC равна:

3. Напряжение на катушке UL, наоборот, опережает по фазе силу тока на π/2. Амплитуда:

Напряжение источника равно сумме напряжений на резисторе, катушке и конденсаторе:

Подставляя сюда выражения (1)–(3), получим:

Вот теперь нам и понадобится метод вспомогательного угла. Выражение во внешних скобках имеет для этого подходящий вид: a sin ωt + b cos ωt. Пользуясь методом вспомогательного угла, получим:

где

Угол α является сдвигом фаз между напряжением источника и силой тока в цепи: фаза напряжения больше фазы тока на величину α. Амплитуда напряжения:

Получив все эти результаты, мы их несколько переиначим.

Начнём с напряжения источника. Предположим, как и ранее, что оно меняется по закону синуса:

Как мы сейчас выяснили, фаза тока меньше фазы напряжения на величину α:

При этом амплитуда силы тока находится из формулы (7):

Выражение (8) имеет вид закона Ома:

где

Величина X — это полное сопротивление цепи. Такое сопротивление оказывает наш колебательный контур переменному току.

Закон Ома в данном случае выполнен лишь для амплитудных значений тока и напряжения. Мгновенные значения I(t) и U(t) уже не будут пропорциональны друг другу — ведь между ними имеется сдвиг фаз, равный α.