Поток вектора напряженности для электрического поля в вакууме. Теорема Гаусса

Поток вектора напряженности для электрического поля в вакууме

Рассмотрим поверхность, ограниченную контуром и помещенную в однородное электростатическое поле . Выбор поверхности и ее ориентация в пространстве определяется единичным вектором нормали , проведенным к данной поверхности. Тогда ориентированную элементарную площадь поверхности можно представить как

Элементарным потоком вектора напряженности электростатического поля через элементарную площадку называется скалярное произведение векторов и

где α – угол между вектором нормали к поверхности и вектором напряженности электростатического поля (рис. 1)

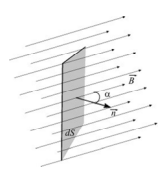
Рис 1. Определение ориентации элемента поверхности dS в электростатическом поле

Выбор направления вектора n условный, так как его можно направить в любую сторону. Единицей потока вектора напряженности электростатического поля является В·м.

Для произвольной замкнутой поверхности S поток вектора E сквозь эту поверхность равен:

где интеграл берется по замкнутой поверхности S.

Поток является алгебраической величиной, он зависит как от конфигурации поля , так и от выбора направления . Для замкнутой поверхности за положительное направление нормали принимается внешняя нормаль, то есть нормаль, направленная наружу области, охватываемой поверхностью. Поэтому пересечения линий напряженности с замкнутой поверхностью, которые выходят из поверхности, следует брать со знаком плюс (угол α – острый) и со знаком минус, если линии входят внутрь (угол α – тупой).

Из рис. 2 видно, если линии проходят внутри замкнутой поверхности непрерывно, каждая линия, пересекая поверхность, входит внутрь и выходит наружу одинаковое число раз. В итоге поток вектора через эту поверхность будет равным нулю.

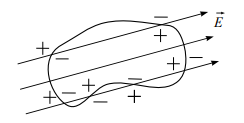
Рис. 2. Определение потока вектора E через замкнутую поверхность

Таким образом, полный поток через замкнутую поверхность

где Nвых и Nвх – число силовых линий, выходящих и входящих в замкнутую поверхность, соответственно.

Возьмем положительный заряд q и окружим его замкнутой поверхностью S произвольной формы (рис. 3).

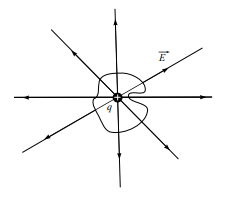
Рис. 3. Картина линий напряженности положительного точечного заряда

Согласно формуле поток

Знак потока совпадает со знаком заряда.

Пусть внутри замкнутой поверхности находится N точечных зарядов q1, q2, …, qN. В силу принципа суперпозиции вектор напряженности результирующего поля равно векторной сумме электрических полей создаваемых в этой точке отдельными зарядами, поэтому

Каждый из интегралов в выражении (1), согласно (2), равен Следовательно,