Работа и мощность тока

Работа тока

Рассмотрим участок цепи, по которому течёт ток I. Напряжение на участке обозначим U, сопротивление участка равно R (рис. 1).

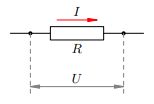
Рис. 1. Участок цепи

За время t по нашему участку проходит заряд q = It. Заряд перемещается стационарным электрическим полем, которое совершает при этом работу:

За счёт работы (1) на рассматриваемом участке может выделяться тепловая энергия или совершаться механическая работа; могут также протекать химические реакции. Короче говоря, данная работа идёт на увеличение энергии нашего участка цепи.

Работа (1) называется работой тока.

Если участок цепи является однородным, т. е. не содержит источника тока, то для этого участка справедлив закон Ома: U = IR. Подставляя это в формулу (1), получим:

Теперь подставим в (1) вместо тока его выражение из закона Ома I = U/R:

Подчеркнём ещё раз: формула (1) получена из самых общих соображений, она является основной и годится для любого участка цепи. А вот формулы (2) и (3) получены из основной формулы с дополнительным привлечением закона Ома и потому годятся только для однородного участка.

Мощность тока

Как вы помните, мощностью называется отношение работы ко времени её совершения. В частности,

Из формул (1)–(3) немедленно получаем соответствующие формулы для мощности тока:

Закон Джоуля–Ленца

Предположим, что на рассматриваемом участке цепи не совершается механическая работа и не протекают химические реакции. Поскольку сила тока постоянна, работа поля не вызывает увеличение кинетической энергии свободных зарядов. Стало быть, работа поля A целиком превращается в тепло Q, которое выделяется на данном участке цепи и рассеивается в окружающее пространство: A = Q.

Таким образом, для количества теплоты, выделяющегося на данном участке цепи, мы получаем формулы:

Но часто бывает так, что не вся работа тока превращается в тепло. Например, за счёт работы тока может совершать механическую работу электродвигатель или заряжаться аккумулятор. Тепло, разумеется, будет выделяться и в этих случаях, но только на сей раз получится, что Q < A (на величину механической работы, совершённой двигателем, или химической энергии, запасённой аккумулятором).

Оказывается, что в подобных случаях остаётся справедливой формула (4). Это — экспериментально установленный закон Джоуля-Ленца.