Резонанс в колебательном контуре
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Резонанс в колебательном контуре
Амплитуда силы тока в контуре зависит от частоты колебаний. Построим график этой зависимости — так называемую резонансную кривую (рис. 1).
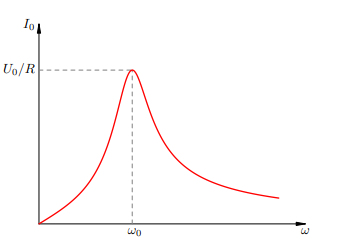
Рис.1. Резонансная кривая
При ω → 0 имеем I0 → 0. Математическая причина стремления силы тока к нулю — неограниченное возрастание ёмкостного сопротивления 1/(ωC), в результате чего полное сопротивление X также стремится к бесконечности. Физическая причина очевидна: ток малой частоты — это почти постоянный ток, а для постоянного тока конденсатор является разрывом цепи.
При ω → ∞ опять-таки имеем I0 → 0: график асимптотически приближается к оси ω. Теперь это происходит за счёт неограниченного роста индуктивного сопротивления ωL. Физическая причина также ясна: при быстром изменении тока в катушке возникает большая ЭДС самоиндукции, препятствующая его увеличению.
При некоторой частоте ω0 амплитуда силы тока достигает максимума: наступает резонанс. Нетрудно видеть, что величина I0 принимает максимальное значение
и происходит это при выполнении равенства
Отсюда находим ω0:
Это хорошо знакомая нам частота собственных колебаний в контуре с нулевым активным сопротивлением. Она же, как видим, является резонансной частотой нашего контура.
Из (1) мы видим, что резонансное значение амплитуды тока I0max тем больше, чем меньше активное сопротивление R. На рис. 2 представлены три резонансные кривые. Верхняя кривая отвечает достаточно малому сопротивлению R, средняя кривая — большему сопротивлению, нижняя кривая — ещё большему сопротивлению.
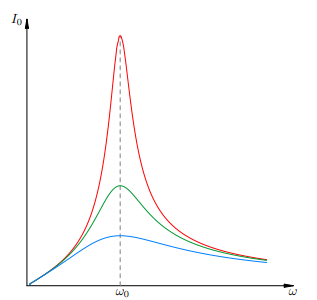
Рис. 2. Резонансные кривые пр Св
Таким образом, резонансный пик тем острее, чем меньше активное сопротивление контура. При весьма большом активном сопротивлении (как это видно из нижней резонансной кривой) понятие резонанса фактически утрачивает смысл.
При резонансе в контуре происходят любопытные вещи.
Амплитуды напряжений на конденсаторе и катушке равны друг другу. Действительно из (2).
При малых значениях R эти амплитуды могут значительно превосходить амплитуду U0 напряжения источника! Это, кстати, является наглядной демонстрацией одного важного факта:
Хотя сумма мгновенных значений напряжения на элементах контура равна мгновенному значению напряжению источника, сумма амплитуд напряжений на отдельных элементах может и не быть равной амплитуде напряжения источника.Равен нулю сдвиг фаз между током в контуре и напряжением источника: α = 0.
Физическую причину синфазности тока и напряжения понять также не сложно. Дело в том, что напряжения Uс и на конденсаторе и катушке колеблются в противофазе (т. е. разность фаз между ними равна π), а их амплитуды при резонансе равны. Стало быть, они отличаются только знаком: = −Uc, и в сумме дают нуль. Получается, что (словно бы в цепи имелся один только резистор), а колебания напряжения и тока на резисторе происходят синфазно.
Резонанс играет важнейшую роль в радиосвязи. Когда осуществляется приём радиосигнала, радиоволны различных частот возбуждают в контуре колебания. Но амплитуды колебаний будут малы для сигналов тех радиостанций, частоты которых отличаются от собственной частоты контура. Контур выделяет лишь ту радиоволну, частота которой равна его собственной частоте; именно эти колебания будут иметь значительную амплитуду.
Поэтому, когда мы настраиваем приёмник на какую-то радиостанцию, мы меняем собственную частоту контура (как правило, путём изменения ёмкости конденсатора), пока не наступит резонанс с искомой радиоволной.
