Равномерное движение по окружности

ДОБАВИТЬ В КОНСПЕКТ

НАВИГАЦИЯ ПО СТРАНИЦЕ

движение точки Вектор скорости ускорение радиан

НАВИГАЦИЯ ПО СТРАНИЦЕ

движение точки Вектор скорости ускорение радиан

Как вам уже известно, равномерным считается движение точки или тела с постоянной скоростью. До этого мы рассматривали равномерное движение по прямой, а теперь рассмотрим тот же вид движения с постоянной скоростью, но по окружности.

А ты знаешь?

Движение точки или тела по окружности является частным случаем криволинейного движения.

Представим, что по окружности мы будем запускать игрушечную машинку.

Вектор скорости машинки направлен по касательной к траектории, которую она описывает. Кроме того, модуль скорости машинки при движении по кругу не меняется, а вот направление вектора скорости будет меняться, когда машинка будет занимать определенные положения по ходу своего движения. (Рисунок 1)

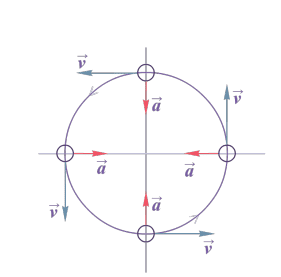
Рисунок 1. Движение точки с постоянной скоростью по окружности

Удивительно, но при таком движении, хоть оно и равномерное, будет существовать некоторое ускорение. Это ускорение всегда будет направлено к центру окружности, и называться оно будет центростремительным (или нормальным). Вычисляться оно будет по формуле: где R — радиус окружности.

При движении по окружности движение машинки будет удобнее описывать не в декартовых координатах, а с помощью радиус-вектора окружности и угла поворота (Рисунок 2)

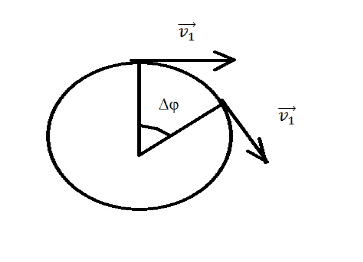
Рисунок 2. Угол поворота при движении по круговой траектории

Угол поворота измеряется в радианах. Вы все уже наверняка знаете, что радиан — это центральный угол, который опирается на дугу, равную радиусу окружности.

Давайте подведем промежуточные итоги (рисунок 3):

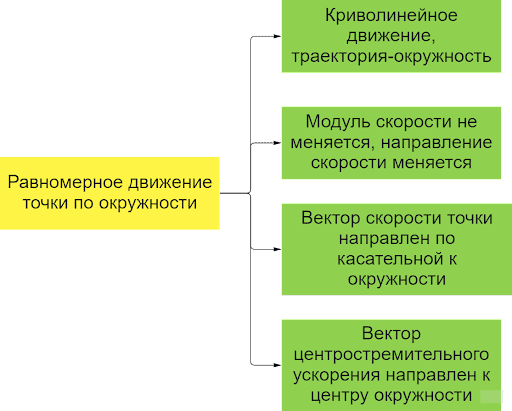
Рисунок 3. Характеристики равномерного движения по окружности