Комбинаторика

• Если слово состоит из K букв, причем есть a1 вариантов выбора первой буквы, a2 вариантов выбора второй буквы и т.д., то число возможных комбинаций букв вычисляется по формуле  (правило умножения).

• Если слово состоит из К букв, причем каждая буква может быть выбрана L способами, то число возможных слов вычисляется как 

В задачах, в которых присутствуют системы счисления, обратить внимание на:

• Число с нуля начинаться не может

• 0 – это четное число

• Не может быть цифры 8 в восьмеричной системе счисления, цифры 6 в шестеричной и тд

Пример задач

• Все 6-буквенные слова, составленные из букв К, Л, О, У, Н, записаны в алфавитном порядке. Вот начало списка:

1. КККККК

2. КККККЛ

3. КККККН

4. КККККО

5. КККККУ

6. ККККЛК

……

Запишите слово, которое стоит на 367-м месте от начала списка. 

Решение:

Перепишем список из задачи в формате числового кода:

Ответ: ККНУОЛ, так как по условию задачи слова шестибуквенные, в начало добавляем незначащие нули, то есть буквы КК

• Все 5-буквенные слова, составленные из букв Д, Ы, Н, Я, записаны в алфавитном порядке. Вот начало списка:

1. ДДДДД

2. ДДДДН

3. ДДДДЫ

4. ДДДДЯ

……

Укажите номер первого слова, которое начинается с буквы Ы. 

Решение: 200004 = 51210

512+1 = 513

Ответ: 513

• Сколько слов длины 4, начинающихся с согласной буквы, можно составить из букв Д, О, М, И, К? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

Решение аналитическим методом:

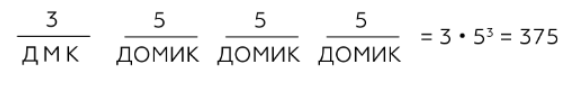
Введем понятия:

Функции библиотеки itertools

Решение с помощью ЯП:

s = 'ДОМИК'

k = 0
for b1 in s:
    for b2 in s:
        for b3 in s:
            for b4 in s:
                s1 = b1 + b2 + b3 + b4
                if b1 in 'ДМК':
                    k += 1

print(k)

k = 0

from  itertools import product

for b in product ('ДОМИК', repeat = 4):

    s = ''.join(b)

    if s[0] in 'ДМК': #склеиваем символы в строки для дальнейшей обработки

        k += 1

print (k)

from  itertools import product

k = len(list(product('ДМК', 'ДОМИК','ДОМИК','ДОМИК'))) 

print (k)

• Виолетта составляет 3-буквенные слова, в которых есть только буквы С, П, А, М, причём буква А используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно имеющая смысл. Сколько существует таких слов, которые может написать Виолетта?

Решение:

Аналитический метод:

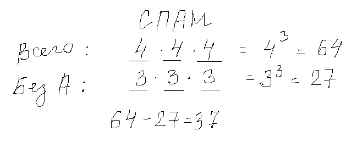
Программный метод:

from  itertools import product

k = 0
for b in product ('СПАМ', repeat = 3):
    s = ''.join(b)
    if s.count('А')>0:
        k += 1

print (k)

• Сколько существует различных символьных последовательностей длины 4 в трёхбуквенном алфавите {К, О, Д}, которые содержат ровно две буквы О?

Количество перестановок одинаковых букв равно:

Аналитический метод	Программа
	from  itertools import product k = 0 for b in product ('КОД', repeat = 4):     s = ''.join(b)     if s.count('О')==2:         k += 1 print (k)

• Аня составляет 7-буквенные коды из букв Л, О, К, Д, А, У, Н. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы У и не может содержать сочетания ОК. Сколько различных кодов может составить Аня?

Раз буквы используются по одному разу, то берем функцию permutations. Аргумента у нее не будет, так как раз все буквы используются по одному разу, то длина слова совпадет с количеством букв в нем.

Аналитический метод	Программа
	from  itertools import  permutations k = 0 for b in permutations ('ЛОКДАУН'):     s = ''.join(b)     if s[0]!='У' and 'ОК' not in s:             k += 1 print (k)

• Мирон составляет 7-буквенные коды из букв Р, А, Р, И, Т, Е, Т. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы И и не может содержать сочетания АР. Сколько различных кодов может составить Мирон?

Сложность задачи в том, что буквы в алфавите Р, А, Р, И, Т, Е, Т повторяются. Функция permutations не обрабатывает повторяющиеся элементы, поэтому вводим новую алгоритмическую структуру SET (множество) – структура данных, в которой хранятся только уникальные значения.

Программа будет выглядеть так:

from  itertools import  permutations
k = 0
for b in set(permutations ('РАРИТЕТ')):
    s = ''.join(b)
    if s[0]!='И' and 'АР' not in s:
            k += 1
            print(s)
print (k)