Обработка целых чисел, делимость числа. Оптимизация программного кода

Поиск делителей числа

Назови делители числа 12? Это 1, 2, 3, 4, 6, 12

Как ты их получил(а)? 

Ты перебирал(а) все числа от 1 до самого числа 12 и проверял(а), делится ли число 12 на все эти числа без остатка. Если делится, то это и есть наш искомый делитель.

А теперь давай это же самое запишем в виде программы:

Обрати внимание, цикл выполняет 12 кругов (итераций).

Пока числа небольшие программа работает молниеносно. Но иногда они переваливают за сотни миллионов.

Так что придется оптимизировать этот код.

Несложно заметить, что делители не превышают «половины» нашего числа N (делители числа 12: от 1 до 6, что и является половиной от 12). Соответственно нет смысла гнать наш счетчик по второй «половине числа». Код уже соответственно будет выглядеть так:

Обрати внимание, цикл выполняет уже 6 кругов (итераций). Но, к сожалению, такое число как 12 слишком далёко от реальностей ЕГЭ 25.

Рассмотрим окончательный оптимизированный вариант поиска делителей, основу которого мы возьмем для отработки задач.

Здесь нужно обратить внимание на то, что у делителей всегда есть пары. Например, наше же число 12 с делителями: 

Что это за пары чисел? Это те числа, произведение которых, дает рабочее число N. Поэтому в алгоритм добавляется команда расчета второго делителя для того, который мы вычислили в условном операторе if

По примеру выше, как ты понимаешь, если у каждого делителя есть пара, значит общее количество делителей числа N — число четное. 

А когда может быть общее количество делителей числа нечетным числом?

В том случае, когда у какого-то числа нет пары. Или же, иначе говоря, оно само для себя является парой. Мы говорим о числах N, которые представляют собой полный квадрат какого числа, например M. Если взять N = 36, то пары делителей 1 и 36, 2 и 13, 3 и 12, 4 и 9 и есть 6 – число квадрат которого дает число N

Отсюда легко делаем вывод, что нечетное количество делителей только у квадратов.

Определение, является ли число простым

Иначе говоря, простое число – это то число, у которого нет делителей на промежутке [2,N].

• Все простые числа, кроме 2 являются нечетными числами.

• 1 – не простое число.

Вот и один из вариантов программы для определения простоты числа:

Можно оформить эту же функцию немного иначе, но смысл при этом не меняется!

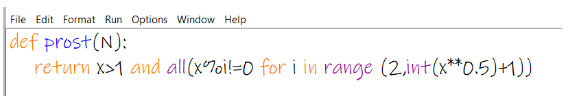
Еще теория:

Основная теорема арифметики говорит о том, что любое число единственным образом (с точностью до порядка сомножителей) единственным образом представимо в виде произведения простых чисел: 

Здесь pi – простые делители, ai – степени делителей

Следствия:

Количество делителей равно:

Например, возьмем 48

, значит число делителей будет (4+1) (1+1) = 10 (см. выше – так и есть!)

Что нам это дает?

1. Если число имеет ровно 5 нечётных делителей (количество четных – любое), в его разложение на простые множители может входить только 1 нечётное простое число. Тогда этими делителями будут , а само число имеет вид , где k – натуральное число или ноль, Здесь и далее p – нечётное простое число.

2. – дает 5 четных делителей (сами делители – ).

3. – дает 3 четных делителя (сами делители ).

В помощь:

If int(x**0.5)**2 == x #если число является полным квадратом