Принцип неопределенности и его свойства
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
То обстоятельство, что в квантовой механике не существует понятия траектории, составляет содержание так называемого «принципа неопределенности», сформулированного в 1927 г. Гейзенбергом.
Принцип неопределенности
Если пытаться измерить одновременно координату и импульс микрочастицы, то чем с большей точностью известно положение частицы, тем больше неопределенность в значении импульса.
С математической точки зрения данное положение обычно записывают в следующем виде:
где — неопределенность координаты , — неопределенность импульса в направлении оси (аналогично для других направлений). Подобное же соотношение существует и для энергии:
которое означает, что
чем короче время существования какого-то состояния или время, отведенное для его наблюдения, тем с меньшей определенностью можно говорить об энергии этого состояния. Если состояние стационарно, то оно может существовать бесконечно долго.
Иногда это соотношение трактуют таким образом: для измерения энергии с точностью необходимо время .
Соотношение неопределенностей не связано с несовершенством измерительных приборов, а глубоко обусловлено самой природой вещей. Если бы оказалось возможным преодолеть это ограничение, то рухнуло бы все здание квантовой механики.
Проанализируем в связи с этим мысленный эксперимент по одновременному определению координаты и импульса электронов при их наблюдении в «гамма-лучевом микроскопе», впервые рассмотренный самим Гейзенбергом.
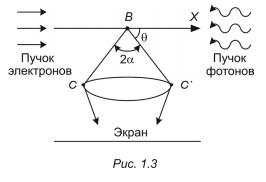
Пусть в направлении оси Х (рис. 1.3) движется свободный электрон. Используем для определения координаты электрона микроскоп. Поскольку требуется высокая точность, будем вести наблюдение с помощью коротких электромагнитных волн. При рассеянии фотонов на электроне в точке В пучок рассеянных фотонов попадает на экран через объектив CC′. В этом случае изображением светящейся точки (электрона) в плоскости изображения является дифракционная картина, состоящая из концентрических колец, окружающих центральный светлый дифракционный кружок (кружок Эйри). На него приходится около 84 % энергии света. Этот кружок и будет изображением светящейся точки (электрона). В волновой оптике доказывается, что минимальное разрешаемое расстояние (определяемое пределом разрешения микроскопа) равно:
Минимальное разрешаемое расстояние
где — угол, под которым виден объектив из положения электрона (так называемая апертура), — длина волны света. Этот предел разрешения обусловлен волновой природой света и не может быть превзойден никакими техническими усовершенствованиями микроскопа. Значение и можно принять за неопределенность координаты электрона . Значение , где — диаметр объектива, — расстояние от электрона до объектива. Таким образом, неопределенность координаты электрона будет порядка .
При рассеянии фотона на электроне происходит изменение состояния самого электрона. Если электроны свободны, то, согласно теории эффекта Комптона
Эффекта Комптона
Импульс, теряемый световым квантом при рассеянии, передается электрону.
Таким образом, если квант света с частотой и импульсом рассеивается на угол , электрону передается импульс, равный
Импульс передаваемый электрону
Следовательно, нельзя наблюдать электрон, не возмущая его. Более того, величина этого возмущения неизвестна, так как из-за конечной апертуры объектива неизвестен сам угол (этот угол может лежать в пределах от XBC до XBC′ ). Значит, для угла есть неопределенность порядка , а поскольку , неопределенность импульса, переданного электрону, будет порядка
Неопределенность импульса, переданного электрону
что и следует из соотношения неопределенностей.
Выводы
Отметим некоторые выводы, вытекающие из соотношения неопределенностей.
Измерения в квантовой области принципиально отличаются от классических измерений. Конечно, и те и другие измерения сопровождаются некоторой ошибкой. Однако в классической физике всегда предполагалось, что путем улучшения методики и техники измерений ошибки могут быть сделаны сколь угодно малыми. В квантовой же механике существует предел точности измерений, который лежит в природе вещей и не может быть преодолен никаким ухищрениями. Соотношения неопределенностей Гейзенберга и устанавливают один из таких пределов. Взаимодействие между макроскопическим прибором и микрочастицей во время измерения принципиально нельзя сделать сколь угодно малым. Если измеряется, например, координата частицы, то измерение неизбежно приводит к неустранимому неконтролируемому искажению первоначального состояния частицы, а следовательно, и к неопределенности импульса при последующем измерении. То же самое происходит, если поменять местами порядок измерения координаты и импульса частицы.
Невозможно реализовать состояние, в котором частица находится в полном покое.
В квантовой механике теряет смысл деление полной энергии на кинетическую и потенциальную. Одна из них зависит от импульсов, а другая от координат. А эти переменные не могут иметь одновременно определенные значения. Энергия должна определяться и измеряться лишь как полная энергия, без деления на кинетическую и потенциальную.
Соотношение неопределенности
Соотношение неопределенности является одним из фундаментальных положений квантовой механики. Оно, например, позволяет объяснить, почему электрон не падает на ядро, более того, оценить даже размеры простейшего атома и его минимальную энергию. Примем для оценки неопределенность положения электрона в атоме водорода порядка размеров атома и неопределенность импульса порядка самого импульса: и . Тогда в силу соотношения неопределенности имеем . В гауссовой системе единиц энергия электрона в атоме водорода равна
Энергия электрона в атоме водорода
Найдем размеры атома при минимальной энергии. Для этого продифференцируем энергию по расстоянию и положим производную равной нулю:
Размер атома водорода
Отсюда сразу находим выражение для боровского радиуса:
Боровский радиус атомы водорода
и для минимальной энергии электрона в атоме водорода
Минимальная энергия атома водорода
Докажем теперь, что электрон не может находиться внутри атомного ядра.
Если электрон может находиться в области порядка размеров ядра (), то неопределенность импульса будет порядка
Оценим теперь его кинетическую энергию. На всякий случай воспользуемся релятивистской формулой для кинетической энергии:
(мы не ошиблись, применив релятивистскую формулу, поскольку полученное значение более чем в 500 раз превосходит энергию покоя электрона). Мы не знаем в природе сил, величина которых обеспечила бы связь электронов, обладающих столь большой энергией, с нуклонами ядра (электростатическая потенциальная энергия электрона на поверхности ядра составляет лишь 10 МэВ).
Представление о классическом движении электрона по орбитам также противоречит соотношению неопределенностей. Чтобы такое представление имело смысл, необходимо выполнение соотношения , где – радиус первой боровской орбиты, а – его неопределенность. Соответствующая неопределенность в радиальном импульсе будет:
что равно самому импульсу электрона . Это и означает, что бессмысленно говорить о движении электрона по орбитам внутри атома.
Посмотрим теперь на колебания атомов в твердых телах с точки зрения принципа неопределенности. Обычно такие колебания связаны с тепловым движением атомов. Чем выше температура, тем сильнее колебания и тем больше амплитуда этих колебаний. При понижении температуры уменьшается и амплитуда этих колебаний. И при нулевой температуре, с точки зрения классической физики, амплитуда должна быть равна нулю. А что же происходит на самом деле? Уменьшение амплитуды колебаний приводит к уменьшению области локализации частицы, и соответственно, в силу принципа неопределенности, начинает расти импульс и энергия частицы. То есть попытка остановить частицу безуспешна! И даже при абсолютном нуле температуры атомы в твердом теле совершают колебания – их называют нулевыми колебаниями.
Оценим энергию этих колебаний, принимая атом за гармонический осциллятор. Энергия гармонического осциллятора массой и частотой связана с амплитудой колебаний A соотношением:
Данное соотношение в сочетании с принципом неопределенности дает своеобразную связь амплитуды колебаний и энергии частицы. Чем меньше энергия, тем меньше амплитуда (область локализации частицы), тем больше минимальный импульс частицы, а это, соответственно, приводит к росту энергии. Минимальная энергия, которой может обладать частица, составляет
Связь амплитуды колебаний и энергии частицы
(при этом мы воспользовались соотношением ).
Из последнего соотношения получаем (точный расчет дает ). Полученный результат говорит о том, что энергия колебаний максимальна у легких атомов, у которых большая частота .
Самое яркое проявление нулевых колебаний – жидкость, которая не замерзает при K. Ясно, что жидкость не замерзает, если кинетической энергии колебаний атомов достаточно для того, чтобы разрушить кристаллическую решетку. При этом совершено неважно происхождение кинетической энергии – связана ли она с тепловым движением атомов или с нулевыми квантовыми колебаниями. Наиболее вероятные кандидаты в незамерзающие жидкости – водород и гелий (максимальная энергия нулевых колебаний). Но гелий – инертный газ, с очень слабым взаимодействием между атомами. И кинетической энергии нулевых колебаний достаточно для расплавления кристаллической решетки. Вот почему гелий не замерзает даже при нулевой температуре при нормальном давлении (при давлении 25 атмосфер гелий все-таки замерзает!).
Иногда соотношение неопределенности получает следующее толкование: «на самом деле» частица имеет точное значение координаты и импульса, однако вмешательство прибора «портит» их значения. Такое истолкование является совершенно неверным, т.к. противоречит наблюдаемой на опыте дифракции микрочастиц.
