Координатный метод
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Вектор
Суть координатного метода решения заключается в том, что ты делаешь привязку к исследуемым фигурам декартовой системы координат (ДСК), затем записываешь векторы, которые образуют ребра исследуемых фигур, и после вычисляешь необходимые величины (их длину или, например, угол между ними). Записывают: Длина отрезка, изображающего вектор, называется модулем вектора и обозначается как Точка — начало вектора, — конец вектора

Прямоугольная система координат в пространстве
Если ты через точку пространства проведешь три попарно перпендикулярные прямые, на каждой из них выберешь направление и выберешь единицу измерения отрезков, то ты задашь систему координат в пространстве.
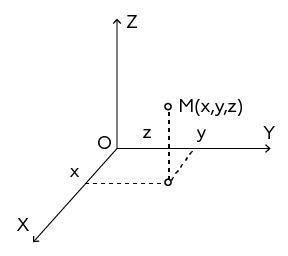
Прямые — координатные оси, точка — начало СК (системы координат). В прямоугольной СК каждой точке пространства сопоставляется тройка чисел — ее координаты. где — абсцисса, — ордината, — аппликата.
Вектор в пространстве
В прямоугольной системе координат в пространстве векторы
— единичные координатные векторы (или орты).
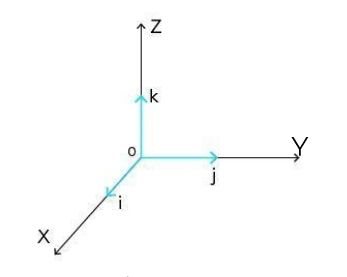
Любой вектор можно разложить по координатным векторам:
Коэффициенты разложения определяется единственным образом.
Алгоритм решения задач с помощью координатного метода
Алгоритм решения задач с помощью координатного метода включает в себя следующие шаги:
выбери такую систему координат, в которой будет удобно получить координаты нужных векторов;
найди координаты необходимых для решения точек;
реши задачу с использованием определенных формул.

Чтобы найти угол между двумя произвольными прямыми, используй формулу:
или в координатной форме:
где — координаты вектора — координаты вектора
Если выполняется тождество: или то можно сделать вывод, что прямые, которым принадлежат данные векторы, перпендикулярны между собой.
Вектор нормали
Нормальный вектор плоскости — это любой ненулевой вектор, который обязательно перпендикулярен этой плоскости.
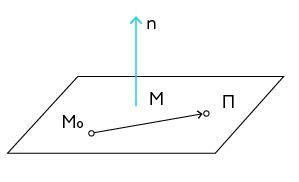
— нормальный вектор плоскости П, — фиксированная точка плоскости П.
Точка принадлежит плоскости П в том случае, если выполняется тождество:
Вырази скалярное произведение векторов в координатах, и получишь общее уравнение плоскости:
или
Угол между прямой и плоскостью
Углом между плоскостью и не перпендикулярной ей прямой называется угол, который находится между этой прямой и ее проекцией на данную плоскость.
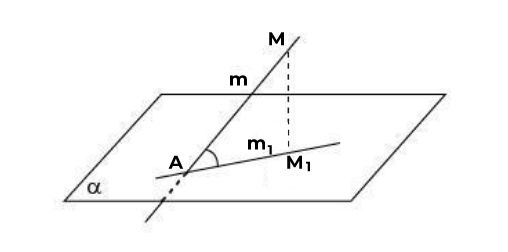
Угол между прямой и плоскостью α ты можешь вычислить :
По формуле где точка принадлежит прямой точка — точка пересечения прямой и плоскости
По формуле где — вектор нормали плоскости — направляющий вектор прямой
Угол между плоскостями
Угол между двумя пересекающимися плоскостями можно вычислить так:
По формуле где точка принадлежит плоскости прямая — прямая, по которой пересекаются плоскости и
По формуле где — вектор нормали плоскости — вектор нормали плоскости
Расстояние от точки до плоскости
Расстояние от точки до плоскости, не содержащей эту точку, равно длине отрезка перпендикуляра, который опустили из этой точки на плоскость.
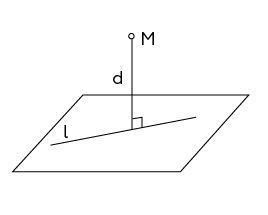
Расстояние от точки до плоскости вычисляется по формуле:
где — уравнение плоскости
