Свойства логарифма

ДОБАВИТЬ В КОНСПЕКТ

НАВИГАЦИЯ ПО СТРАНИЦЕ

Логарифмом числа свойства логарифмов логарифмического тождества перехода к новому основанию

ПОЛНЫЙ ОТВЕТ

БЕЗ ВОДЫ

Без воды — краткий вариант ответа,
легко понять и запомнить

НАВИГАЦИЯ ПО СТРАНИЦЕ

Логарифмом числа свойства логарифмов логарифмического тождества перехода к новому основанию

Обычно на этом моменте возникает тяжелый вздох, так как сложно осознать, что вообще такое логарифм. С этого и начнём! Легче всего прочувствовать необходимость в логарифмах на решении показательного уравнения графическим способом. Начерти график и с его помощью реши уравнения:

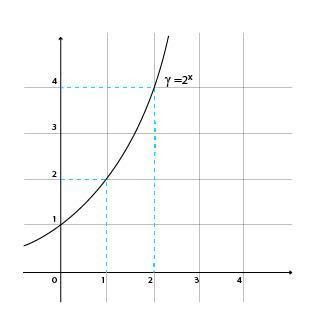
Отлично! А теперь реши уравнение И здесь возникают сложности, ведь из графика видно, что корень уравнения больше 1 и меньше 2, однако даже подбирая десятичные дроби, ты не найдешь точного значения, только приближенные.

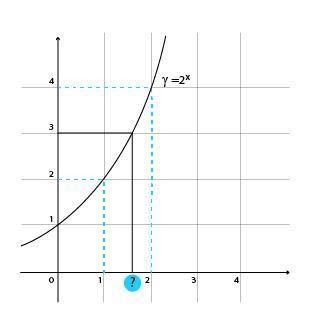
В данном случае корень не будет ни целым, ни дробным, ни иррациональным числом, а задать его можно с помощью логарифма, а именно

Логарифмом числа по основанию называют показатель степени с основанием равной То есть, можно сказать, что логарифм — это степень, в которую нужно возвести для получения Но не забывай, логарифм не просто степень, он сложнее, соответственно у него есть ограничения.

Ограничения:

Кроме разнообразных логарифмов, есть два, которые отличаются своим видом и написанием.

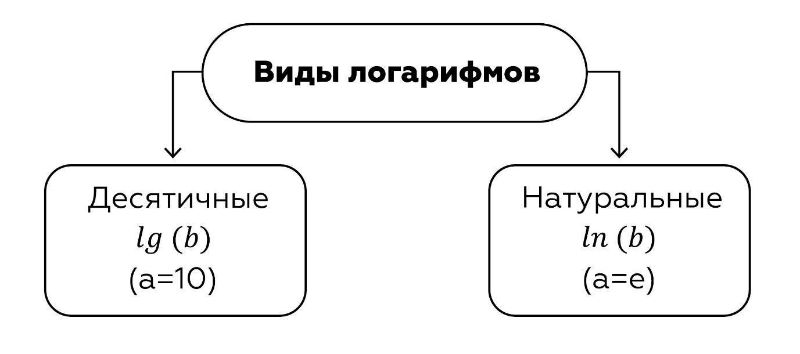
Вспомним свойства логарифмов:

Эта формула носит название основного логарифмического тождества. Именно эта формула тебе будет помогать при решении логарифмических уравнений и неравенств, когда число нужно будет представить в виде логарифма.
При сложении\вычитании логарифмов с одинаковыми основаниями, показатели перемножаются\делятся соответственно.
Если в показатели или в основании логарифма стоит степень, то её показатель выносится по следующим правилам:
Эта формула имеет название формулы перехода к новому основанию. То есть от основания можно перейти к любому допустимому основанию А следующая формула является частным случаем формулы перехода к новому основанию, если нужно поменять основание и показатель местами.

Кстати,что эта формула является частным случаем прошлой формулы, очень легко доказать:

Пример:

Найти значение выражения
Решение: Данное выражение, убрав множитель представляет собой левую часть основного логарифмического тождества, используя его, получишь
Найти значение выражения
В показателе логарифма можно увидеть произведение и следовательно применимо свойство, позволяющее представить этот логарифм в виде суммы логарифмов, а дальше в показателе логарифма стоит степень, что также поддается упрощению, и используй определение логарифма напоследок: