Точки экстремума функции и промежутки монотонности
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Точки экстремума функции
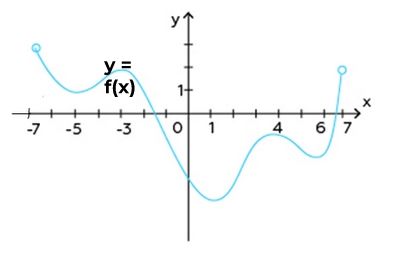 |  |
Алгоритм нахождения точек экстремума:
Первым делом найди область определения и интервалы, на которых функция непрерывна.
Теперь, используя таблицу производных и правила дифференцирования, найди производную функции.
Чтобы получить уравнение, которое нужно решить, приравняй производную к нулю.
Отметь полученные критические точки .
У каждого промежутка определи знак производной.
Выполни проверку относительно каждой критической точки: эта точка — точка максимума или точка минимума?
Еще раз внимательно прочитай вопрос задания, проверь решение и запиши ответ.
Поведение производной | Поведение функции |
Возрастает | |
Убывает | |
Точки экстремумов: |
*Если в точке производная ноль и меняет знак с «+» на «-», то это точка максимума. А если в точке производная ноль и меняет знак с «-» на «+», то это точка минимума функции.
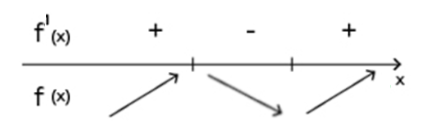
Признаки возрастания и убывания функции
Возрастание функции Функция возрастает, если при увеличении аргумента значение функции увеличивается. | Убывание функции Функция возрастает, если при увеличении аргумента значение функции уменьшается. |
 |  |
Алгоритм нахождения наименьшего/наибольшего значения функции:
Первым делом найди область определения и интервалы, на которых функция непрерывна. Если тебе задан определенный отрезок, убедись, что он входит в область определения функции.
Найди производную, используя таблицу производных.
Приравняй производную к нулю. Теперь у тебя получилось уравнение, которое нужно решить.
Выбери критические точки, которые принадлежат данному отрезку.
В критических точках нужно вычислить значение функции.
На концах отрезка вычисли также значение функции.
Сравни полученные результаты, чтобы выбрать из них наименьшее или наибольшее значение в соответствии с вопросом задания. Если тебе задан определенный отрезок, убедись, что выбранная тобой точка входит в него.
