Модуль Юнга

Характеристикой жесткости материалов являются модули упругости.

Около 1800 г. английский ученый Томас Юнг (Thomas Young, 1773—1829 гг.) пришел к выводу, что если пользоваться не абсолютными значениями сил и смещений в конструкциях, а напряжениями и деформациями, то закон Гука можно записать в следующем виде:

где — модуль деформации при линейном растяжении твердого тела (модуль Юнга):

Модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия. Модуль Юнга численно равен напряжению деформации, вызывающему единичную деформацию, т. е. растяжение твердого тела на единицу (увеличение размера твердого тела в 2 раза).

Для большинства широко распространенных материалов модуль Юнга определен экспериментально. Чем больше модуль Юнга, тем меньше деформируется стержень при прочих равных условиях.

Подставив в формулу 1 выражения и :

Обозначим жесткость стержня:

тогда:

Жесткость k стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.

Частное проявление закона Гука: сила упругости, возникающая при деформации пружины (рис. 1), прямо пропорциональна удлинению пружины:

где x — удлинение пружины; k — постоянный коэффициент, называемый жесткостью пружины, «минус» означает, что сила упругости направлена в сторону, противоположную перемещению частиц при деформации пружины, т. е. в сторону, противоположную удлинению x пружины.

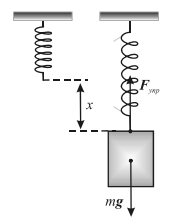
Рис. 1. Деформация растяжения пружины. Fупр = −mg, Fупр = −kx

При пластических деформациях твердых тел наблюдается явление упругого гистерезиса.

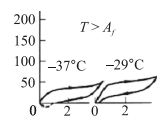
Рис. 2. Диаграммы «напряжение-деформация» сплава CuZn

При повторном действии силы на твердое тело, испытавшее пластическую деформацию, с ростом напряжения деформации σ относительная деформация ε снова растет в соответствии с законом Гука с тем же значением модуля Юнга, т. е. с тем же наклоном прямой, но предел упругости теперь будет равен тому максимальному напряжению, которым закончилось первое деформирование.