Модули сдвига и объёмного сжатия. Коэффициент Пуассона

Модули сдвига и объёмного сжатия. Коэффициент Пуассона

Пластическая деформация приводит к повышению предела упругости твердого тела, т. е. к его упрочению.

Упрочение, которое достигается в результате пластической деформации, может быть устранено, если подвергнуть деформированное тело длительному нагреву при высокой температуре. Этот прием называют отжигом деформации.

Линейное растяжение или сжатие твердого тела сопровождается изменением его поперечного размера (рис. 1). Эту деформацию характеризуют относительной деформацией поперечного размера (сечения):

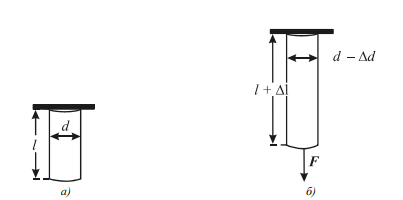
Рисунок 1. Изменение поперечного размера

Модуль объемного сжатия (модуль объемной упругости, объемный модуль упругости, модуль всестороннего сжатия) K характеризует способность материала сопротивляться изменению его объема, не сопровождающемуся изменением формы (рис. 2). Он равен отношению величины нормального напряжения к величине относительного объемного сжатия θ, вызванного этим напряжением:

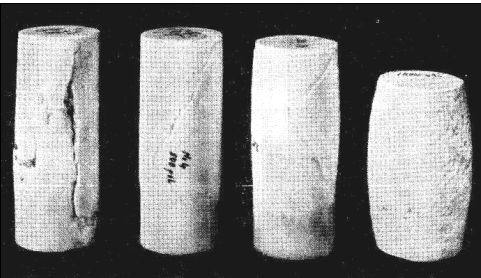
Рисунок 2. Образец мрамора после деформации при различных величинах всестороннего давления (1 бар, 35 бар, 300 бар, 1000 бар)

Модуль объемного сжатия K всегда несколько меньше, чем модуль Юнга E. При деформации сдвига величину смещения называют абсолютным сдвигом одной грани относительно другой грани. Угол γ деформации называют углом сдвига, а тангенс угла γ — относительным сдвигом.

Модуль сдвига G характеризует способность материала сопротивляться изменению формы при сохранении его объема. По величине он равен отношению касательного напряжения τ к величине угла сдвига γ, определяющего искажение прямого угла между плоскостями, по которым действуют касательные напряжения:

где S — площадь грани; G — модуль сдвига. Можно показать, что G < 0,5 E.

Отношение между относительной величиной деформации поперечного размера и относительной величиной линейной деформации твердого тела (рис. 1) называют коэффициентом поперечных деформаций (коэффициентом поперечного сжатия, коэффициентом Пуассона) ν:

Величина ν определяет относительное изменение объема деформируемого твердого тела, зависит от материала тела и является одной из важных постоянных, характеризующих его упругие свойства. Коэффициент Пуассона всегда меньше 0,5. У большинства материалов ν близок к 0,5.

Перечисленные характеристики упругих свойств функционально связаны между собой следующими соотношениями:

Таким образом, зная две из этих характеристик, можно рассчитать значения двух других. Обычно для горных пород экспериментально определяют характеристики E и ν.

Интересно отметить, что такую же пару характеристик, по которым можно определить остальные параметры упругости однородного массива, представляют его плотность и скорость распространения в нем упругих колебаний (сейсмической волны).

Модуль Юнга E и коэффициент Пуассона ν полностью характеризуют упругие свойства твердого тела при определенной температуре, т. е. в изотермических условиях.

Упругие свойства среды могут быть также определены другими парами констант, например, постоянными Лямэ λ и µ, скоростями распространения продольных и поперечных волн.

Постоянные Лямэ

Постоянные Лямэ связаны с модулем Юнга E и коэффициентом Пуассона ν следующими соотношениями:

Все сказанное, строго говоря, справедливо лишь для однородных изотропных тел. Реальные тела редко бывают однородными. Но современная техника позволяет выращивать макрокристаллы, обладающие большой однородностью. Поэтому пределы упругости и прочности у них гораздо выше, чем у поликристаллов.

Всестороннему сжатию могут подвергаться не только твердые тела, но и жидкости и газы. У воды K = . На дне Мирового океана, на глубине порядка 4 км, давление p приблизительно равно Твердые тела с их жесткой кристаллической решеткой значительно менее сжимаемы по сравнению с жидкостями, атомы и молекулы которых не так сильно связаны со своими соседями. Сжимаемость газов на много порядков выше, чем у жидкостей и твердых тел. Величина модуля объемного сжатия определяет скорость звука в данном веществе.