Неравномерное движение

Начнём с равномерного движения. Пусть скорость тела постоянна и равна . Возьмём два момента времени: начальный момент и конечный момент . Длительность рассматриваемого промежутка времени равна . Очевидно, что за промежуток времени тело проходит путь:

Давайте построим график зависимости скорости от времени при равномерном движении. В данном случае это будет прямая, параллельная оси абсцисс (рис.1).

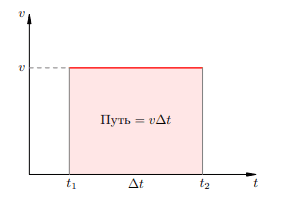
Рисунок 1. Путь при равномерном движении

Нетрудно видеть, что пройденный путь равен площади прямоугольника, расположенного под графиком скорости. В самом деле, первый множитель в формуле есть вертикальная сторона этого прямоугольника, а второй множитель ∆t — его горизонтальная сторона. Теперь нам предстоит обобщить эту геометрическую интерпретацию на случай неравномерного движения. Пусть скорость тела зависит от времени, и на рассматриваемом промежутке график скорости выглядит, например, так(рис.2):

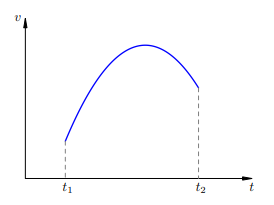
Рисунок 2. Неравномерное движение

Дальше мы рассуждаем следующим образом.

1. Разобьём наш промежуток времени на небольшие отрезки величиной ∆t.

2. Предположим, что на каждом таком отрезке тело движется с постоянной скоростью. То есть, плавное изменение скорости заменим ступенчатой аппроксимацией: в течение каждого небольшого отрезка времени тело движется равномерно, а затем скорость тела мгновенно и скачком меняется. На рис. показаны две ступенчатые аппроксимации. Ширина ступенек ∆t на правом рисунке вдвое меньше, чем на левом. Путь, пройденный за время ∆t равномерного движения — это площадь прямоугольника, расположенного под ступенькой. Поэтому путь, пройденный за всё время такого «ступенчатого» движения — это сумма площадей всех прямоугольников на графике.

3. Теперь устремляем ∆t к нулю. Ясно, что в пределе наша ступенчатая аппроксимация перейдёт в исходный график скорости на рис. 1. Сумма площадей прямоугольников перейдёт в площадь под графиком скорости; следовательно, эта площадь и есть путь, пройденный телом за время от до (рис. 4).

На рис. 3 показаны две ступенчатые аппроксимации. Ширина ступенек ∆t на правом рисунке вдвое меньше, чем на левом.

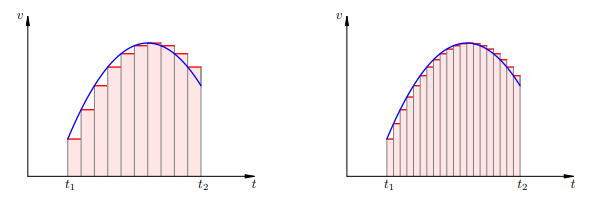
Рисунок 3. Ступенчатая аппроксимация

Путь, пройденный за время ∆t равномерного движения — это площадь прямоугольника, расположенного под ступенькой. Поэтому путь, пройденный за всё время такого «ступенчатого» движения — это сумма площадей всех прямоугольников на графике.

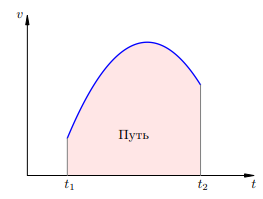
Рисунок 4. Путь при неравномерном движении