Парадокс часов

Парадокс часов

Поразительным и вызывающим большое число споров и недоразумений является так называемый «парадокс часов». Пусть часы A находятся в точке 1 в неподвижной инерциальной системе отсчета K, а в точности такие же часы B, находившиеся в начальный момент также в точке 1, движутся к точке 2 со скоростью v. Затем, пройдя путь L до точки 2, часы B возвращаются и, приобретая противоположную скорость −v, возвращаются в точку 1 (рис. 1).

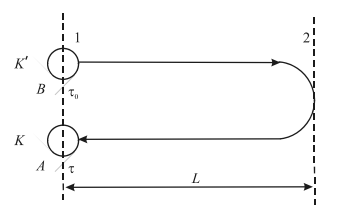
Рис. 1. Парадокс часов

Если время, требуемое на изменение скорости v движущихся часов B на обратную (−v), достаточно мало по сравнению со временем прямолинейного и равномерного движения от точки 1 до точки 2, то время, за которое часы B проходят весь путь 1-2-1, отмеренное часами A, и время, отмеренное часами B, можно вычислить по формулам:

где δ — возможная малая поправка на время ускоренного движения часов B. Следовательно, часы B, вернувшись в точку 1, реально отстанут от часов A на время:

Особенность этого кинетического следствия преобразований Лоренца состоит в том, что здесь отставание хода движущихся часов является вполне реальным эффектом, а не результатом избранной процедуры измерения. Реально должны замедляться все процессы, происходящие в системе K′, по сравнению с процессами, идущими в системе K. В том числе должны отставать и биологические процессы организмов, находящихся вместе с часами B. То есть должны замедляться и физиологические процессы в организме человека и животных, путешествующих в системе K′, в результате чего организм, находившийся в системе в момент ее возврата в точку 1, окажется менее постаревшим, чем организм, оставшийся в системе.

Парадоксальным представляется здесь то, что одни из часов реально отстают от других. Ведь это кажется противоречащим самому принципу относительности, т. к. согласно последнему любую из систем K и K′ можно считать неподвижной. Но тогда представляется, что лишь в зависимости от нашего выбора реально отстающими могут стать любые из часов A и B. Но последнее явно абсурдно, т. к. реально отстают часы B от часов A.

Ошибочность последнего рассуждения состоит в том, что системы K и K′ физически не равноправны, т. к. система K все время инерциальна, система же K′ некоторый промежуток времени, когда производится изменение ее скорости на обратную, неинерциальна. Следовательно, вторая из формул (1) для системы K′ неприменима, т. к. во время ускорения ход удаленных часов может сильно измениться за счет инерциального гравитационного поля.

Однако и это совершенно правильное объяснение представляется весьма поразительным. Ведь в течение большого промежутка времени обе системы движутся друг относительно друга прямолинейно и равномерно. Поэтому, с точки зрения системы K′, часы A, находящиеся в K, отстают (но не уходят вперед) в полном соответствии с формулой (1). И лишь за малый промежуток времени, когда в системе K′ действуют силы инерции, часы A быстро уходят вперед на промежуток времени, вдвое больший, чем Δτ. При этом, чем большее ускорение испытывает система K′, тем быстрее бежит время на часах A.

По измерениям наблюдателя, находящегося в инерциальной системе K, в движущейся со скоростью v инерциальной системе K′ течение времени замедляется.