Потенциальная энергия. Формулы потенциальной энергии деформированной пружины
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Потенциальная энергия тела вблизи поверхности Земли
Рассмотрим тело массы m, находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем. Если тело находится на высоте h, то
где g — ускорение свободного падения вблизи поверхности Земли.
Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже, физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства. Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки P, находящейся на высоте h1, в точку Q, находящуюся на высоте h2 (рис. 1)
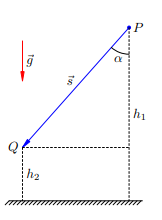
A = mg(h1 − h2)
Угол между силой тяжести и перемещением тела обозначим α. Для работы силы тяжести получим:
Но, как видно из рис. 1.,. Поэтому
или
Учитывая, что , имеем также:
Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.
Сила называется
Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.
Потенциальная энергия деформированной пружины
Рассмотрим пружину жёсткости k. Начальная деформация пружины равна . Предположим, что пружина деформируется до некоторой конечной величины деформации . Чему равна при этом работа силы упругости пружины? В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат. Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин и определяется формулой:
Величина
называется потенциальной энергией деформированной пружины (x — величина деформации). Следовательно,
