Прямолинейное равноускоренное движение
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Графиком равноускоренного движения является
Производная вектора скорости есть вектор ускорения:
В нашем случае имеем = const. Чтобы получить постоянный вектор , нужно продифференцировать функцию . Но не только: к ней нужно добавить ещё произвольный постоянный вектор (ведь производная постоянного вектора равна нулю),в нашем случае . Таким образом:
В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. При проекции уравнения на ось OX получаем скалярную величину:
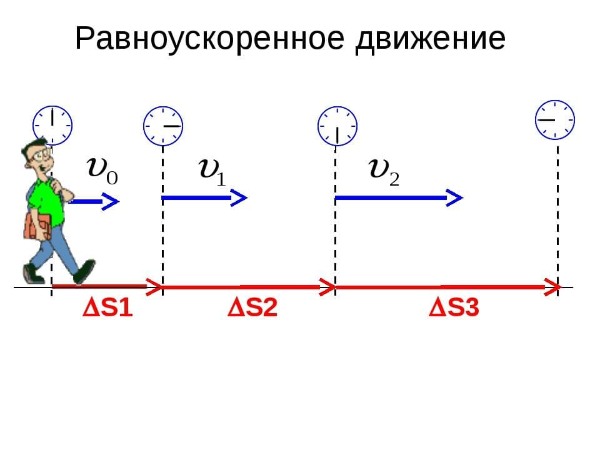
Равноускоренное движение
Закон движения
Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела. Подставляем сюда выражение для скорости:
Продифференцируя это равенство, получаем:
Переходя к проекциям на координатную ось, получаем скалярное неравенство:
Заметим, что — перемещение тела. Тогда получаем зависимость перемещения от времени:
Если выразить из 3 формулы t и подставить в формулу для перемещения:
Эта формула не содержит времени t и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.
