Равномерное движение по окружности
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Пусть точка вращается по окружности радиуса r. Скорость точки постоянна по модулю и равна v. Скорость v называется линейной скоростью точки.
Для периода T имеем очевидную формулу:
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду). Пусть, например, T = 0,1 с. Это означает, что за время 0,1 с точка совершает один полный оборот. Частота при этом равна: ν = 1/0,1 = 10 об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат O в центре окружности
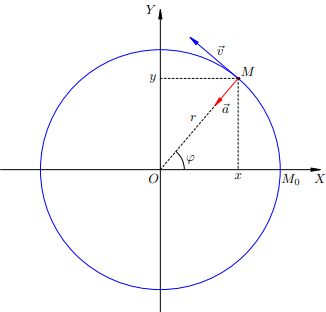
Равномерное движение по окружности
Пусть M0 — начальное положение точки; иными словами, при t = 0 точка имела координаты (r, 0). Пусть за время t точка повернулась на угол и заняла положение M.Отношение угла поворота ко времени называется угловой скоростью вращения точки:
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с.
За время, равное периоду вращения, точка поворачивается на угол 2π. Поэтому
Сопоставляя формулы, получаем связь линейной и угловой скоростей:
