Сила тяжести
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Время: 3.44-5.42
Предположим, что тело находится вблизи некоторой планеты.
В подавляющем большинстве случаев сила тяжести — это сила притяжения к Земле.
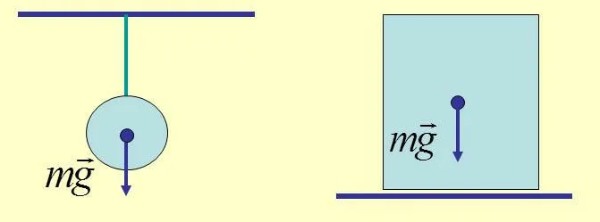
Рисунок 1. Сила тяжести
Пусть тело массы m лежит на поверхности Земли. На тело действует сила тяжести mg, где g — ускорение свободного падения вблизи поверхности Земли. С другой стороны, считая Землю однородным шаром, можно выразить силу тяжести по закону всемирного тяготения:
где M — масса Земли, R ≈ 6400 км — радиус Земли. Отсюда получаем формулу для ускорения свободного падения на поверхности Земли:
Эта же формула, разумеется, позволяет найти ускорение свободного падения на поверхности любой планеты массы M и радиуса R. Если тело находится на высоте h над поверхностью планеты, то для силы тяжести получаем:
Здесь g — ускорение свободного падения на высоте h:
Искусственные спутники
Для того, чтобы искусственный спутник мог совершать орбитальное движение вокруг планеты, ему нужно сообщить определённую скорость. Найдём скорость кругового движения спутника на высоте h над поверхностью планеты. Масса планеты M, её радиус R.
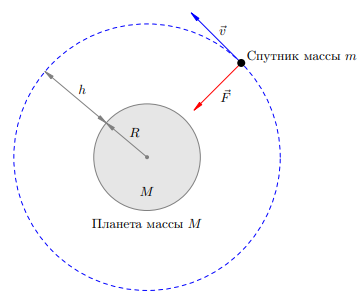
Рисунок 2.Спутник на круговой орбите
Спутник будет двигаться под действием единственной силы — силы всемирного тяготения, направленной к центру планеты. Туда же направлено и ускорение спутника — центростремительное ускорение.
Обозначив через m массу спутника, запишем второй закон Ньютона в проекции на ось, направленной к центру планеты: ma = F, или
Отсюда получаем выражение для скорости:
Для первой космической скорости имеем:
или, с учётом формулы
Для Земли приближённо получаем 8000 м/с = 8 км/с.
