Силы упругости. Закон Гука

На данном уроке мы будем изучать закон Гука, определим такие понятия, как деформация и сила упругости. Таймкод: 0:00 Тема и план урока 0:17 Деформация тел 1:55 Сила упругости 3:01 Закон Гука 4:09 Графическое представление 4:38 Итоги Понравилось, как преподаватель объясняет материал? Получи ещё больше полезного контента о подготовке к экзаменам в наших соц.сетях: https://clck.ru/Zr7kn - канал в Дзене, где разбираем сложные темы в образовании https://vk.com/domy24 - паблик ВК, в котором постоянно проводят розыгрыши и конкурсы А обо всём, что мы делаем, можно узнать у нас на сайте: https://center-think.ru/

Деформация

Силы упругости возникают при деформациях тел.

К деформациям относятся:

• растяжение;

• сжатие;

• кручение;

• сдвиг;

• изгиб;

Деформации бывают упругими и неупругими (пластическими). Упругая деформация полностью исчезает после снятия внешнего воздействия, которое вызвало деформацию. В результате деформированное поначалу тело восстанавливает свои первоначальные размеры и форму.

Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме. Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов).

Силы взаимодействия зависят от расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается. Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.

Сила упругости

Сила упругости:

1. действует между соседними слоями деформированного тела и приложена к каждому слою;

2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры);

Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения.

Закон Гука

Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.

Закон Гука

Абсолютная величина силы упругости прямо пропорциональна величине деформации.

В частности, для пружины, сжатой или растянутой на величину x, сила упругости 54 даётся формулой:

где k — коэффициент жёсткости пружины. Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров. Из формулы следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1):

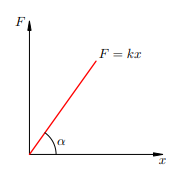
Рисунок 1. Закон Гука

Коэффициент жёсткости k — это угловой коэффициент в уравнении прямой F = kx. Поэтому справедливо равенство:

Модуль Юнга

В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид закона Гука. Именно, если стержень длиной l и площадью поперечного сечения S растянуть или сжать на величину x, то для силы упругости справедлива формула:

Здесь E — модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.