Сложение векторов
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Коллинеарные векторы — векторы, лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Нулевой вектор — любая точка плоскости, обозначается как нуль со стрелкой сверху.
Над векторами можно выполнять множество операций, но самая основная из них – сложение.
Сложение векторов
Векторные величины изображаются направленными отрезками (векторами) могут складываться по 3 правилам:
Правило треугольника.
Правило параллелограмма.
Правило многоугольника.
1. Правило треугольника
Для этого нужно начало вектора (рис. 1 а) совместить с концом вектора , их суммой будет вектор (рис. 1 б), соединяющий начало вектора с концом вектора .
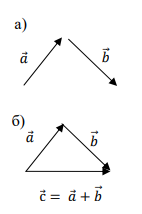
Рисунок 1. Правило треугольника
2. Правило параллелограмма
Для того чтобы сложить два вектора по правилу параллелограмма, необходимо:
Взять произвольную точку А.
Отложить от точки векторы и .
Построить на векторах и параллелограмм.
Диагональ параллелограмма и будет суммой векторов (рис. 2)
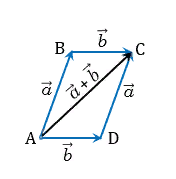
Рисунок 2. Правило параллелограмма
3. Правило многоугольника
Если начало очередного вектора соединить с концом предыдущего, то получим ломаную линию (рис. 3). Вектор , проведенный из начала первого вектора в конец последнего, является суммой нескольких векторов (в данном случае четырех): ܽ
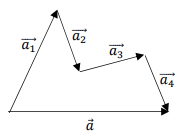
Рисунок 3. Правило многоугольника
