Теорема Гюйгенса–Штейнера

Теорема Гюйгенса–Штейнера

Момент инерции тела зависит от выбора оси вращения. Однако это не значит, что для всякой новой оси момент инерции I следует вычислять заново, пользуясь формулой.

Пусть момент инерции твердого тела относительно оси С, проходящей через его центр инерции, известен и равен . Можно показать, что относительно оси AA, параллельной оси CC (рис. 1), он равен:

где m — масса твердого тела; l — расстояние между осями.

Выражение (1) представляет собой теорему Гюйгенса—Штейнера (теорему Штейнера):

Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

Теорема Штейнера сводит вычисление момента инерции относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела.

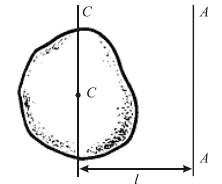
Рис. 1. К теореме Гюйгенса—Штейнера

Приведем значения моментов инерции для некоторых тел (тела предполагаются однородными, масса тела — m).

Суммирование в проводится по всем материальным точкам, образующим тело. Практически вычисление такой суммы сводится к вычислению соответствующего интеграла, что для однородных тел симметричной формы, когда ось вращения совпадает с осью симметрии (проходит через центр массы), обычно является несложной задачей. Так, в случае тонкого стержня длины l относительно оси, перпендикулярной к стержню и проходящей через его середину, момент инерции равен ; тонкого стержня длины l относительно оси, перпендикулярной к стержню и проходящей через его конец, — ; тонкостенного цилиндра (обруча) относительно оси, совпадающей с осью трубы, — ; сплошного цилиндра (диска) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр, —; шара относительно оси, совпадающей с диаметром, —(рис. 2); тонкого диска (толщина диска во много раз меньше радиуса диска) —; круглого цилиндра длины l относительно оси, перпендикулярной к оси цилиндра и проходящей через его середину, – . Определение момента инерции тел сложной конфигурации связано с большими математическими трудностями, поэтому их часто определяют опытным путем.

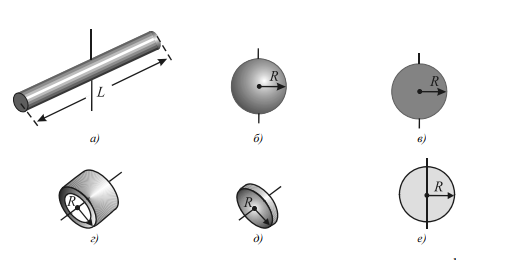
Рис. 2. Моменты инерции некоторых тел