Теорема Торричелли. Эффект Магнуса

Теорема Торричелли

Пусть жидкость налита в широкий сосуд, в котором внизу, в боковой стенке, находится отверстие на расстоянии h от свободной поверхности жидкости (рис. 1). Если сосуд широкий, а отверстие небольшое, то изменением h за время вытекания жидкости можно пренебречь. Можно также приближенно считать, что скорость течения жидкости в верхнем сечении равна нулю.

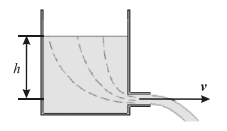
Рис. 1. Истечение жидкости из широкого сосуда

Давления в обоих сечениях одинаковы (и равны атмосферному давлению). Уравнение Бернулли в этом частном случае упрощается:

откуда следует, что:

т. е. жидкость вытекает со скоростью свободного падения с высоты h (теорема Торричелли).

Пусть жидкость течет по горизонтальной трубе, в которой сечение суживается, тогда h = const и

Скорость течения в узком месте больше, поэтому давление в нем меньше (рис. 2). На этом свойстве основано устройство струйного насоса. В струйном насосе жидкость (газ) перемещается, увлекаемая потоком (струей) жидкой или газообразной среды. В зависимости от вида струи различают жидкоструйные (например, водоструйные), газо- и пароструйные насосы. КПД до 40%.

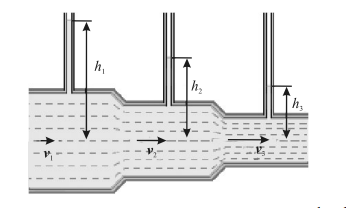
Рис. 2. Изменение давления в потоке жидкости. v1<v2<v3,h1>h2>h3

Уравнение Бернулли для газов. Эффект Магнуса

В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе.

Уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.

Одной из таких задач является изучение сил, действующих на крыло самолета. Строгое теоретическое решение этой задачи чрезвычайно сложно, и обычно для исследования сил применяются экспериментальные методы. Уравнение Бернулли позволяет дать лишь качественное объяснение возникновению подъемной силы крыла.

Из-за специального профиля крыла и наличия угла атаки, т. е. угла наклона крыла по отношению к набегающему потоку воздуха, скорость воздушного потока над крылом оказывается больше, чем под крылом (рис. 2). Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила F, действующая на крыло. Вертикальную составляющую Fy этой силы называют подъемной силой. Подъемная сила удерживает летящий самолет в воздухе. Горизонтальная составляющая Fx представляет собой силу сопротивления среды.

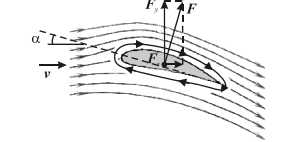
Рис. 3. Линии тока при обтекании крыла самолета и возникновение подъемной силы. α — угол атаки

Жуковский показал, что существенную роль при обтекании крыла играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение (циркуляция) воздуха вокруг крыла. В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего потока, в нижней части эти скорости направлены в противоположные стороны. Это и приводит к возникновению разности давлений и появлению подъемной силы.

Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха, вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета (рис. 4). Это явление называют эффектом Магнуса (открыт немецким физиком Генрихом Густавом Мáгнусом). Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в волейбол, футбол или теннис.