Уравнение Бернулли

Уравнение Бернулли

Рассмотрим ламинарное стационарное (т. е. форма и расположение линий тока, а также значения скоростей в каждой точке со временем не изменяются) течение несжимаемой (идеальной) жидкости внутри узкой трубки тока, ограниченной поперечными сечениями и (рис. 1). Пусть в сечении скорость жидкости , а в сечении скорость . За промежуток времени Δt рассматриваемый объем сместится на расстояние в сечении и на расстояние в сечении . Так как по предположению жидкость несжимаема, то при перемещении ее объем не изменяется:

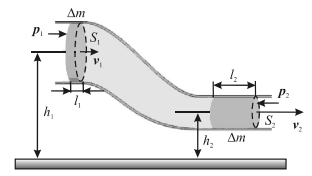
Рисунок 1. Течение идеальной жидкости по трубе переменного сечения. Условие несжимаемости

Скорость течения несжимаемой жидкости обратно пропорциональна площади поперечного сечения трубки тока; в разных сечениях скорости относятся как обратные значения сечений.

Изменение энергии рассмотренного объема равняется совершенной над ним работе внешних сил. Внешними силами являются силы давления со стороны остальной части жидкости. Изменение положения объема за время Δt определяется тем, что объем при ламинарном течении несжимаемой жидкости перешел в равный ему объем ; массы этих объемов Δm равны, т. к. жидкость несжимаема, а, следовательно, плотность жидкости всюду одинакова:

Разность энергий объемов и равна работе внешних сил. Так как полная энергия складывается из кинетической и потенциальной энергий, то можно написать:

где и — высóты, занимаемые объемами и над некоторым произвольно выбранным уровнем.

Если давления в первом и втором сечениях равны и соответственно, то (работа внешних сил во втором сечении отрицательна, т. к. силы давления противоположны направлению скорости). Поэтому:

Подставляя в (2) выражение для Δm из (1), сокращая на и перенося члены для первого объема влево, а члены для второго объема направо, получим:

Если (труба горизонтальная), то:

Поскольку выбор сечений был произвольным, сумма величин остается постоянной в любом сечении:

Зависимость давления идеальной жидкости от скорости ее течения в математической форме была впервые установлена швейцарским ученым Даниилом Бернýлли (Daniel Bernoulli, 1700—1782 гг.) в 1726—1738 гг.