Закон сохранения импульса
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Система тел называется
Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами. Равнодействующая внешних сил, приложенных к замкнутой системе, равна нулю: = 0. В этом случае получаем:
Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:
Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
стрелок ощущает отдачу при выстреле из ружья;
рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
шары сталкиваются на бильярдном столе.
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
Возьмем замкнутую систему из двух взаимодействующих тел. Силы и — это силы взаимодействия между телами. Третий закон Ньютона гласит, что . Пусть тела взаимодействуют во течение времени t. Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.
По второму закону Ньютона:
Здесь — скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.
Из записанного выше следует соотношение:
Это равенство — математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
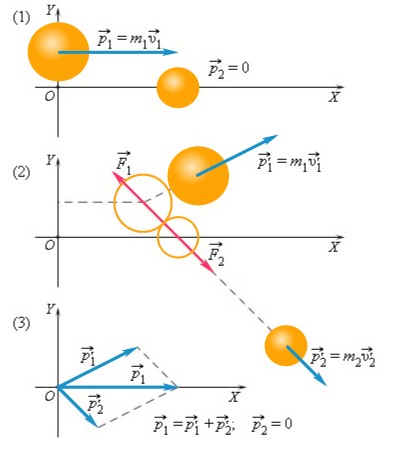
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
