Барометрическая формула. Распределение Больцмана. Закон Максвелла-Больцмана
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Барометрическая формула
Атмосферное давление на какой-либо высоте обусловлено весом слоёв газа, лежащих выше. Пусть – давление на высоте , а - на высоте .
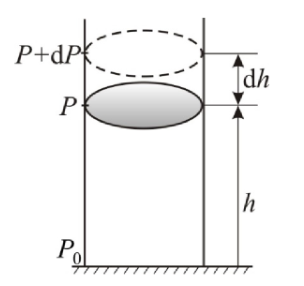
Давление P, P+dP на высотах h, h+dh соответственно
Разность давления равна весу газа, заключённого в объёме цилиндра с площадью основания, равной единице, и высотой .
Так как , где — плотность газа на высоте , медленно убывающая с высотой, то можно записать: .
Отсюда можно получить барометрическую формулу, показывающую зависимость атмосферного давления от высоты:
Из барометрической формулы следует, что давление убывает с высотой тем быстрее, чем тяжелее газ (чем больше и чем ниже температура. Например, на больших высотах концентрация легких газов и гораздо больше, чем у поверхности Земли.
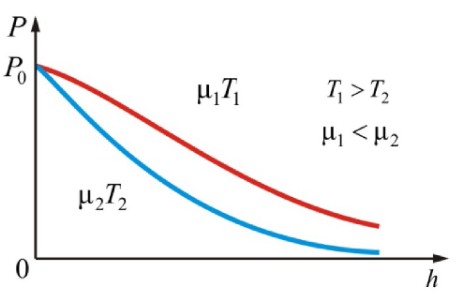
Зависимость давления от высоты при разных молярных массах и температурах
Распределение Больцмана
Исходя из основного уравнения молекулярно-кинетической теории , заменим и в барометрической формуле на и и получим распределение молекул во внешнем потенциальном поле – распределение Больцмана:
где и – число молекул в единичном объёме на высоте и .
С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия , то на разных высотах – различна. Следовательно, уравнение (3.2.5) характеризует распределение частиц по значениям потенциальной энергии:
Данное уравнение является законом распределения частиц по потенциальным энергиям — распределение Больцмана.
Закон Максвелла-Больцмана
Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии, а закон Больцмана – распределение частиц по значениям потенциальной энергии. Учитывая, что полная энергия , оба распределения можно объединить в единый закон Максвелла-Больцмана:
