Функция распределения Максвелла
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Функция распределения Максвелла
Пусть имеется n тождественных молекул, находящихся в состоянии беспорядочного теплового движения при определенной температуре. После каждого акта столкновения между молекулами их скорости меняются случайным образом. В результате невообразимо большого числа столкновений устанавливается стационарное равновесное состояние, когда число молекул в заданном интервале скоростей сохраняется постоянным.
Распределение молекул идеального газа по скоростям впервые было получено знаменитым английским ученым Дж. Максвеллом в 1860 г. с помощью методов теории вероятностей.
Функция распределения Максвелла характеризует распределение молекул по скоростям и определяется отношением кинетической энергии молекулы к средней энергии её теплового движения :
Эта функция обозначает долю молекул единичного объёма газа, абсолютные скорости которых заключены в интервале скоростей от до +Δ, включающем данную скорость.
Обозначим множитель перед экспонентой через , тогда из представленного уравнения получим окончательное выражение функции распределения Максвелла:
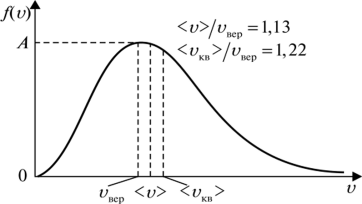
График функции распределения Максвелла
На графике функции показаны наиболее вероятная, среднеарифметическая и среднеквадратичная скорости газовых молекул.
Средние скорости распределения Максвелла
Из графика функции распределения Максвелла, видно, что наиболее вероятная скорость – скорость, на которую приходится максимум зависимости.
Наиболее вероятная скорость молекулы:
Среднеарифметическая скорость молекулы:
Среднеквадратичная скорость молекулы:
Зависимость функции распределения Максвелла от массы молекул и температуры газа
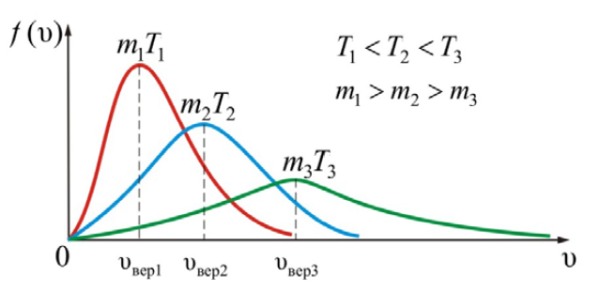
Максвелловское распределение молекул
На рисунке показано, что при увеличении массы молекул (m1 > m2 > m3) и при уменьшении температуры (T1 < T2 < T3) максимум функции распределения Максвелла смещается вправо, в сторону увеличения скоростей.
Площадь под кривой – величина постоянная, равная единице, поэтому важно знать, как будет изменяться положение максимума кривой:
~, кроме того ~
Выводы:
Вид распределения молекул газа по скоростям зависит от рода газа и от температуры. Давление P и объём газа V на распределение молекул не влияют.
В показателе степени f(v) стоит отношение кинетической энергии, соответствующей данной скорости, к средней энергии теплового движения молекул; значит, распределение Максвелла характеризует распределение молекул по значениям кинетической энергии.
Максвелловский закон – статистический, и выполняется тем лучше, чем больше число молекул.
Формула Максвелла для относительных скоростей
Относительную скорость обозначим через .
Тогда получим закон распределения Максвелла в приведенном виде:
Это уравнение универсальное. В таком виде функция распределения не зависит ни от рода газа, ни от температуры.
