Закон о равномерном распределении энергии по степеням свободы

Закон о равномерном распределении энергии по степеням свободы

Положение одноатомной молекулы, как и материальной точки, задается тремя координатами, поэтому она имеет три степени свободы (рис. 1).

Многоатомная молекула может еще и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два независимых вращения, а любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомной молекулы вращение вокруг ее собственной оси не изменит ее положение в пространстве, а момент инерции относительно этой оси равен нулю (рис. 1).

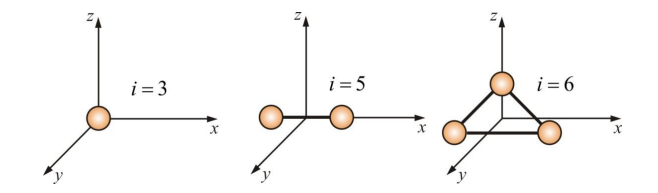
Рис. 1. Число степеней свободы одно-, двух- и трехатомных молекул

Таким образом, у двухатомных молекул пять степеней свободы (i = 5), а у трехатомных – шесть степеней свободы (i = 6).

Итак, если частица идеального газа простая, то она имеет лишь три степени свободы поступательного движения. Ее энергия равна 3kT/2. Если же частица идеального газа сложная, то она обладает большим числом степеней свободы и, следовательно, большей энергией.

Например, если сложная частица состоит из двух точечных частиц, то имеются две возможности. Если две частицы между собой жестко связаны и ведут себя подобно твердой гантели, то сложная частица имеет пять степеней свободы: три поступательные и две вращательные. В этом случае энергия частицы равна 5kT/2. Если же наряду с этим связь между частицами не жесткая и они могут совершать колебательное движение вдоль соединяющей их линии, то добавляются кинетическая энергия kT 2 и потенциальная энергия kT 2 колебаний, т. е. еще две степени свободы. Всего при этом на одну сложную частицу приходится энергия

Л. Больцман доказал, что средняя энергия, приходящаяся на каждую степень свободы, равна kT/2.

Это выражение называется теоремой о равномерном распределении средней энергии по степеням свободы.

В моле имеется частиц, и, следовательно, внутренняя энергия моля идеального газа равна:

Таким образом, если система находится в состоянии термодинамического равновесия, при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы. На каждую поступательную и вращательную степени свободы приходится энергия kT/2. Для колебательной степени свободы она равна kT. Общее число степеней свободы i = iп + iвр + 2iкол.