Дифференциальная зависимость между продольной силой и нагрузкой. Напряжения в поперечном сечении бруса при центральном растяжении (сжатии)

Дифференциальная зависимость между продольной силой и нагрузкой

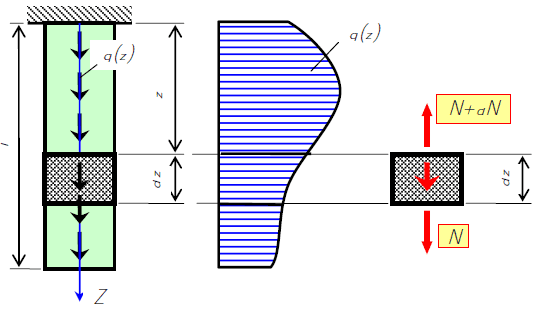
Равновесие элементарного участка стержня, загруженного распределенной нагрузкой

Пусть дан стержень, загруженный распределенной по некоторому закону нагрузкой q(z).

Рассмотрим элементарный участок стержня длиной dz. Учитывая условие равновесия:

получим:

Таким образом, производная от продольной силы N равна интенсивности распределенной нагрузки q. Полученная зависимость используется для проверки эпюры N, а так же для вывода некоторых формул.

Напряжения в поперечном сечении бруса при центральном растяжении (сжатии)

Рассмотрим длинный стержень, испытывающий центральное растяжение

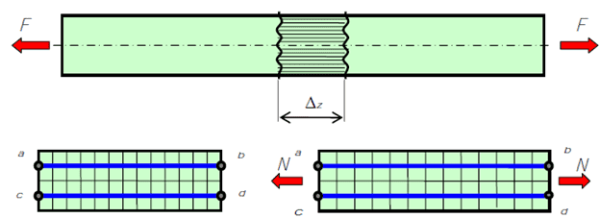
Деформации волокон участка стержня при центральном растяжении длинного стержня

Опыты показывают, что сечение b-d в результате деформации выделенного участка стержня переместиться параллельно само себе, оставаясь при этом плоским. Это означает, что волокна a-b и c-d удлиняются одинаково. Отсюда следует утверждение.

На основании гипотезы Бернулли все продольные волокна стержня деформируются одинаково. Следовательно, напряжения в них также одинаковые, а значит напряжения и по всей площади поперечного сечения распределены равномерно.

Используя зависимость между напряжениями σ и продольной силой N, получим

или

Здесь N – продольная сила в поперечном сечении стержня; A – площадь поперечного сечения.