Главные оси и главные моменты инерции

Рассмотрим сечение произвольной формы. Пусть оси поворачиваются около неподвижной точки C.

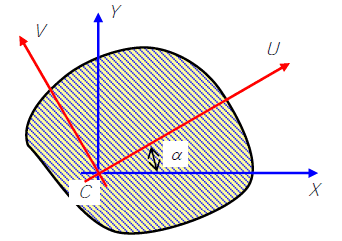
Поворот осей относительно неподвижной точки C

При изменении угла α изменяются и моменты инерции сечения относительно поворачивающихся осей. Так как моменты инерции выражаются непрерывными функциями с аргументом α, то они должны иметь экстремальные значения. Обозначим оси, относительно которых моменты инерции принимают экстремальные значения буквами U и V. Причем условимся — ось с максимальным моментом инерции обозначать буквой U, а ось с минимальным моментом инерции буквой V.

Формула для определения положения двух взаимно перпендикулярных осей, относительно одной из которых момент инерции принимает максимальное значение, а относительно другой — минимальное:

Покажем, что центробежный момент относительно этих осей равен нулю. Для этого найдем угол поворота осей, относительно которых центробежный момент становится равным нулю:

Очевидно, что угол наклона осей с экстремальными моментами инерции и угол наклона осей, относительно которых центробежный момент инерции равен нулю одинаковые. Следовательно, высказанное предположение справедливо. Дадим название этим особенным осям инерции.

Если сечение имеет ось симметрии, то эта ось и ей перпендикулярная ось, неважно является ли она сама осью симметрии или нет, будут главными осями инерции.

Если сечение имеет более чем две оси симметрии, то согласно определению, любая центральная ось является главной центральной осью инерции. Примеры приведены на рисунке.

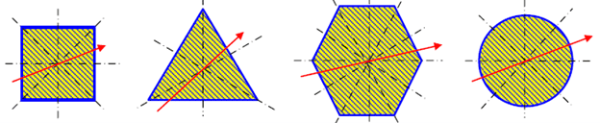
Любая центральная ось для сечений в форме квадрата, равностороннего треугольника, равностороннего многоугольника, круга является главной центральной осью инерции

В некоторых случаях для определения знака или положения объектов удобно использовать правила построения и знаки квадрант координатной плоскости. Отметим, что квадранты образуются разделением координатной плоскости координатными осями на четверти. Квадранты ограничены с двух сторон координатными осями и ограниченны с двух других сторон.

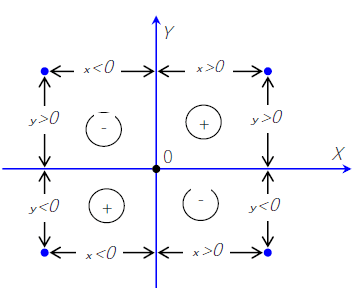
Расстановка знаков на квадрантах координатной плоскости