Касательные напряжения при поперечном изгибе. Формула Журавского

При поперечном изгибе в поперечных сечениях балки кроме изгибающих моментов появляются еще и поперечные силы, а, следовательно, и касательные напряжения. Согласно закону парности касательных напряжений и в продольных сечениях балки будут появляться касательные напряжения. Эти напряжения вызывают сдвиг продольных слоев (волокон) относительно друг друга, что приводит к искривлению поперечных сечений.

Экспериментально установлено, что величина депланации сечения зависит от отношения длины балки к высоте ее сечения.

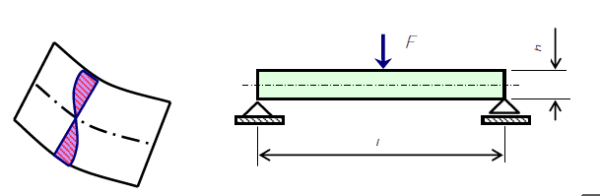
Депланация поперечных сечений за счет касательных напряжений

Различают балки по отношению ее длины к высоте поперечного сечения:

Установлено, что депланация поперечных сечений в тонких балках незначительная и ею можно пренебречь. Поэтому формула для нормальных напряжений в тонких балках при поперечном изгибе вполне приемлема.

Расчет толстых балок (плит) выполняется методами теории упругости и в сопротивлении материалов не рассматривается.

Рассмотрим балку, испытывающую поперечный изгиб.

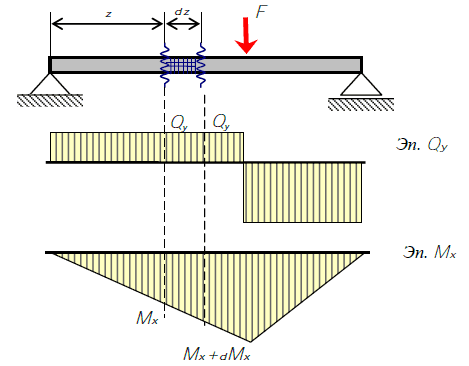
Балка, испытывающая поперечный изгиб

Двумя сечениями выделим элементарный участок на балке и рассмотрим его подробнее.

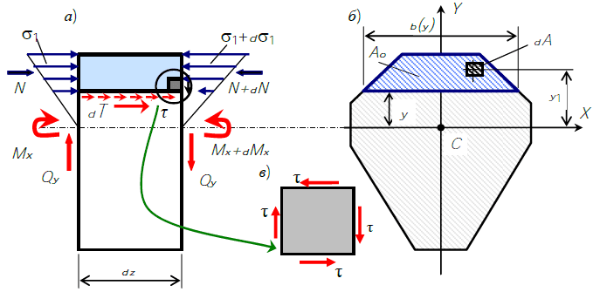
Элемент балка, подвергнутый действию нормальных и касательных напряжений в поперечных и продольных сечениях при поперечном изгибе

В левом сечении изгибающий момент равен , а в правом . Поэтому нормальные напряжения в отмеченной точке отличаются и равны слева:

а справа

Отсюда следует, что изменение нормального напряжения на расстоянии dz равно:

Тогда приращение силы равно:

Поэтому равнодействующую касательных напряжений в горизонтальном сечении можно вычислить по формуле:

Из условия равновесия справедливо равенство:

Подставим выражения для dT и dN и получим:

Отсюда следует выражение для касательного напряжения в продольном сечении балки на выделенном участке:

Учитывая закон парности касательных напряжений, касательные напряжения и в поперечном сечении балки равны:

где

• — поперечная сила в рассматриваемом сечении балки;

• — статический момент отсеченной части сечения относительно нейтральной оси X;

• — момент инерции всего сечения относительно нейтральной оси X;

• b — ширина сечения, на уровне точки в которой вычисляется касательное напряжение.

Максимальные касательные напряжения при поперечном изгибе появляются в точках, расположенных на нейтральной оси.

Полученная формула называется формулой Журавского и предназначена для вычисления касательных напряжений в произвольной точке сечения при поперечном изгибе балки.

Пример распределения касательных напряжений по высоте сечения балки при ее поперечном изгибе.

Примеры распределения касательных напряжений по высоте сечения