Общие понятия о динамических расчетах строительных конструкций
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Некоторые нагрузки на строительные конструкции сравнительно быстро меняют свою величину или положение. Такие нагрузки называются динамическими.
Примеры. Действие поезда на мост, работа штампового пресса, работа машин и механизмов с маховиками, забивка свай копром и др.
Динамические нагрузки вызывают колебательные движения частей сооружений. Поэтому при расчете следует учитывать силы инерции. Отметим, что признаком динамической задачи является необходимость учета сил инерции. При решении динамических задач используются два метода — дифференциальный и интегральный.
Дифференциальный метод основан на составлении дифференциального уравнения динамического равновесия и получение уравнения движения частей сооружения. Анализ уравнения движения позволяет получить ускорения точек сооружения, а значит и сил инерции, которые учитываются в расчете. Этот метод связан с большими математическими проблемами – решением больших систем дифференциальных уравнений.
Так, например, достаточно простая задача динамического расчета однопролетной П-образной рамы при одномассовом сгущении ее элементов потребует решения системы двух дифференциальных уравнений. При этом, вычисляя деформации, следует ограничиться учетом только изгибом элементов рамы.
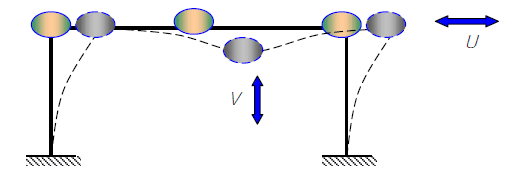
Расчетная схема П-образной рамы для динамического расчета
Интегральный метод основан на использовании динамического коэффициента. Этот метод чаще всего используется при расчете строительных конструкций.
Динамический коэффициент равен отношению исследуемой величины при динамическом воздействии к значению этой же величины при статическом воздействии.
Sст — исследуемая величина при статическом приложении нагрузки (N, M, V, σ и др.);
kд — динамический коэффициент, определяемый аналитически или экспериментально.
Динамический коэффициент зависит от:
вида динамической нагрузки;
размеров конструкции;
массы конструкции;
жесткости элементов конструкции;
и др.
