Основные понятия о степенях свободы и статической неопределимости
НАВИГАЦИЯ ПО СТРАНИЦЕ
Вначале рассмотрим вопрос о возможностях перемещения механических систем – степенях свободы. Это изучалось в курсе теоретической механики. Однако, считаем необходимым повторить это и в курсе сопротивления материалов.
Пусть абсолютно жесткое тело находится в пространства (рис. 88 а). Выберем произвольную систему координатных осей — X, Y, Z. В этом пространстве тело имеет возможность совершить шесть независимых движений – смещения по направлению каждой оси U, V, W и повороты около этих осей α, β, γ. Таким образом, тело имеет шесть степеней свободы.
Теперь, поместим тело уже на плоскости, образованной координатными осями X и Y. Количество независимых движений этого тела равно трем — смещения по направлениям осей X и Y — U и V, а также поворот около начала координат α. Количество степеней свободы равно трем.
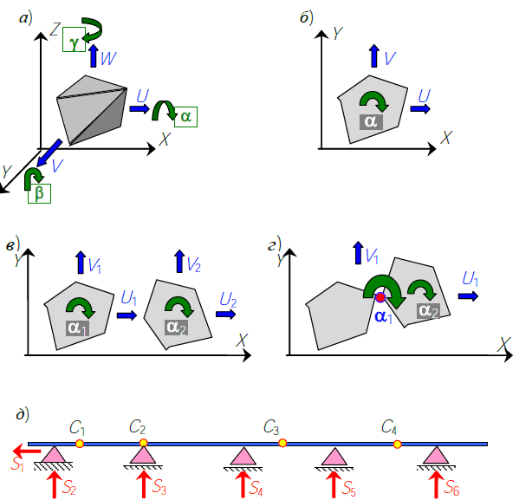
Примеры определения количества степеней свободы
Поместим на плоскость два абсолютно жестких не связанных друг с другом тела. Количество степеней свободы этой системы равно шести — три степени свободы одного тела и три степени свободы другого тела .
Однако, элементы конструкций чаще всего как-то связаны друг с другом и опорой. Каждая связь уменьшает количество степеней свободы на единицу. Соединим два тела шарниром. Полученная система в целом может совершить движения по направлению оси X и оси Y — , а также поворачиваться около начала координат .
Кроме того, одно тело может поворачиваться относительно другого за счет связывающего их шарнира. Таким образом, шарнир уменьшил количество степеней свободы на два. Значит, установленный шарнир ограничивает возможность движений системы на два, то есть шарнир, соединяющий оба тела, имеет две связи.
На рисунке показана балка, разрезанная на пять частей четырьмя шарнирами и опирающаяся на шарнирно неподвижную опору и шарнирно подвижные опоры . Части балки в плоскости, образованной двумя осями X и Y в сумме имеют 15 степеней свободы. Шарнирно неподвижная опора слева и четыре шарнирно подвижные опоры ограничивают возможность шести смещениям системы, а четыре шарнира, каждый из которых имеет по две связи, ограничивают возможность движений по восьми направлениям. Таким образом, система имеет только одну степень свободы 15-6-8=1.
Сделанные выше рассуждения, очень важны при исследовании статически неопределимых механических систем. Дадим определение статически неопределимым системам.
Статически неопределимыми системами называются такие системы, у которых количество неизвестных реакций или внутренних сил превышает число уравнений равновесия.
В этом случае реакции и внутренние силы методами статики найдены быть не могут.
Любая статически неопределимая система характеризуется степенью статической неопределимости, которая равна разности числа неизвестных и числа линейно независимых уравнений равновесия. Статическая неопределимость может быть внутренней и внешней.
Таким образом, для определения неизвестных в статически неопределимых системах следует иметь такое количество уравнений, которое было бы равно числу неизвестных. Если количества уравнений равновесия не хватает, то необходимо дополнительно составить уравнения, но уже не по условию статического равновесия, а из каких-то других соображений, например, по условию совместности деформаций элементов рассматриваемой конструкции. Такие уравнения будем называть дополнительными. Число дополнительных уравнений должно быть равным степени статической неопределимости механической системы.
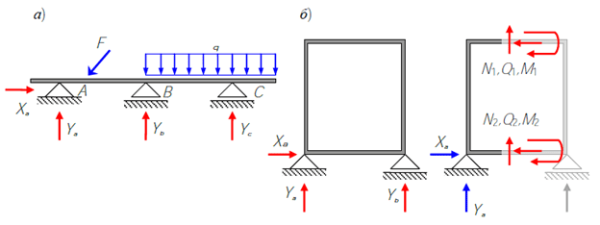
Примеры механических систем с внешней (а) и с внутренней (б) статической неопределимостью
На рисунке показана балка, опирающаяся на три опоры. Левая опора является шарнирно неподвижной и имеет две связи. Поэтому в ней появляются две реакции . Опоры B и C шарнирно подвижные, имеют по одной связи. В каждой из них появляется по одной реакции То есть балка имеет четыре связи. Но балку следует рассматривать как тело расположенное в плоскости. Поэтому она имеет три степени свободы – перемещения по вертикальному и горизонтальному направлениям и поворот около неподвижной точки. Значит, степень статической неопределимости балки равна n=4–3=1 и требуется составить одно дополнительное уравнение.
Дополнительное уравнение присоединяется к трем уравнениям равновесия. В результате получается система, содержащая четыре уравнения, то есть столько, сколько неизвестных. Решением этой системы уравнений, определяются все неизвестные — внешние (реакции) и внутренние (внутренние силы). Рассмотренная балка имеет внешнюю статическую неопределимость.
На рисунке показана рама, расположенная в плоскости XY и опирающуюся на шарнирно неподвижную опору A с двумя связями и шарнирно подвижную опору B, с одной связью. Если рассматривать раму как одно тело, имеющую три степени свободы в плоскости XY, то ее следует рассматривать как статически определимую. В сумме опоры A и B имеют три связи, соединяющие раму с опорой. Поэтому количество уравнений равновесия равно количеству неизвестны сил (реакций) в этих связях. А это значит, что неизвестные реакции могут быть найдены только из уравнений равновесия. Значит рама внешне статически определимая.
Если нам понадобиться найти не только реакции, но и внутренние силы в сечениях рамы, то уравнений статического равновесия не хватит. Вертикальным сечением разделим раму на две части — левую и правую, отбросим правую часть и рассмотрим левую. Отброшенная правая часть действует на левую часть внутренними силами и . То есть всего неизвестных шесть, а уравнений равновесия можно составить только три. Очевидно, что уравнений недостаточно и требуется составить еще три дополнительных уравнения уже не по условию равновесия, а из условия совместности деформаций. Следовательно, рама внутренне трижды статически неопределимая.
Статически неопределимые системы являются более экономичными и часто применяются в строительстве. Однако, расчет таких конструкций более трудоемкий и сложный чем статически определимых конструкций.





