Положение нулевой линии при перемещении точки приложения силы из точки 1 в точку 2

Пусть оси X и Y являются главными центральными осями инерции сечения. Поставим условие, чтобы точка приложения силы () движется по прямой 1-2. Уравнение прямой 1-2 в отрезках имеет вид:

Если сила приложена в точке 1, то нулевая линия будет перпендикулярна оси Y и удалена от оси X на :

Если сила приложена в точке 2, то нулевая линия будет перпендикулярна оси X и удалена от оси Y на :

Вычислим напряжения в точке S при приложения силы в произвольной точке прямой 1-2:

Таким образом, где бы не была приложена сила F на прямой 1-2, напряжение в точке S будет равно нулю. Следовательно, нулевая линия при движении точки приложения силы F по прямой 1-2 будет поворачиваться около неподвижной точки S. Предположение доказано.

Иллюстрация свойств нулевой линии приведена на рисунке.

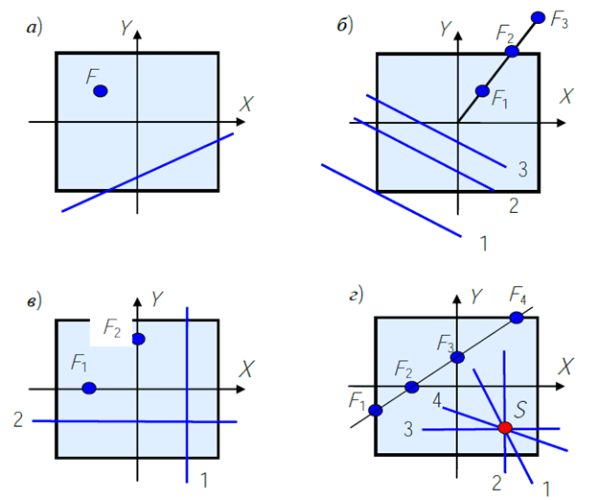
Иллюстрация свойств нулевой линии – первое (а), второе (б), третье (в) и четвертое (г)