Понятие о напряжениях. Связь напряжений и внутренних сил. Вывод зависимостей
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Внутренние силы N, , , , и T в поперечном сечении стержня в действительности не являются сосредоточенными силами. Они распределены по площади сечения по некоторым законам. Определение этих законов является одной из основных задач сопротивления материалов.
Распределение внутренних сил характеризуется их интенсивностью, которая измеряется напряжениями (механическими напряжениями). Введем понятие о напряжениях. Рассмотрим поперечное сечение стержня и напряжения в его точке.
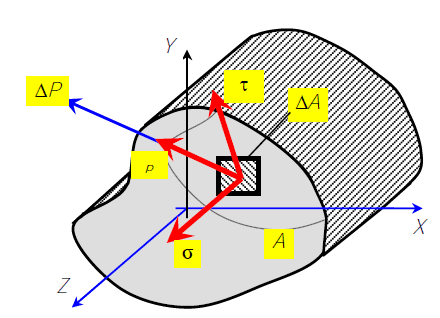
Полное, нормальное и касательное напряжения в точке
Около произвольной точки выделим малую площадку ΔA, через которую передается малая внутренняя сила ΔP.
Полным напряжением p (МПа) в точке называется величина, характеризующая интенсивность внутренней силы, равная пределу отношения внутренней силы ΔP, передающейся через площадку ΔA, если площадь ΔA площадки стремится к нулю.
В расчетах полное напряжение редко используется. Обычно используются нормальное и касательное напряжения.
Нормальным напряжением σ (МПа) в точке называется величина, равная проекции полного напряжения на нормаль рассматриваемой площадки. Если нормальное напряжение вызывает сжатие, то оно считается отрицательным, если вызывает растяжение – принимается положительным.
Касательным напряжением τ (МПа) в точке называется величина, равная проекции полного напряжения на плоскость рассматриваемой площадки. Правило расстановки знаков для касательного напряжения будет рассмотрено позже.
Такое разложение полного напряжения на нормальное и касательное сложилось исторически и вполне обосновано. Опыты показывают, что материалы по-разному сопротивляются растяжению (сжатию) и сдвигу.
Связь напряжений и внутренних сил
Для исследований характера распределения внутренних сил по площади сечения установим связь между внутренними силами и напряжениями. Полагаем, что распределение напряжений в пределах сечения выражается непрерывными функциями.
Элементарная продольная сила, передающаяся через площадку dA равна:
Предполагается, что в пределах элементарной площадки из-за ее малости напряжения σ распределены равномерно. Проинтегрируем левую и правую части записанного выше выражения и получим:
Элементарный момент относительно оси X, вызванный элементарной силой σ⋅dA, передающейся через площадку dA, равен:
Проинтегрируем левую и правую части выражения и получим:
