Продольные и поперечные деформации центрально растянутого (сжатого) бруса
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Рассмотрим длинный стержень, подвергнутый центральному растяжению.
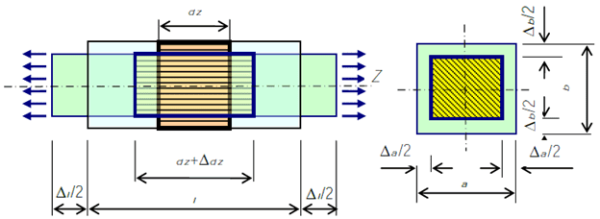
Продольные и поперечные деформации центрально растянутого стержня
Согласно определению относительная продольная деформация волокна равна:
Здесь длина волокна S равна длине элементарного участка dS. Поэтому:
Предел не записывается, потому что дифференциал dz и так стремится к нулю. Из полученной формулы следует:
Согласно гипотезе Бернулли все волокна находятся в одинаковых условиях. Кроме того, будем полагать, что по всей своей длине волокна деформируются одинаково, так как рассматривается длинный стержень. Поэтому ε=const.
Проинтегрируем (то есть просуммируем) деформации по длине волокна и получим:
Окончательно имеем:
Аналогичные рассуждения для поперечных деформаций приводят к выражениям.
Если материал изотропен, то
Отношение относительной поперечной деформации к относительной продольной деформации, взятое по абсолютной величине называется коэффициентом поперечной деформации или коэффициентом Пуассона.
Здесь:
ε’ — относительная линейная поперечная деформация, то есть деформация по направлению перпендикулярному к направлению действия силы или нормального напряжения;
ε — относительная линейная продольная деформация, то есть деформация по направлению действия силы или нормального напряжения.
Коэффициент Пуассона ν — величина безразмерная и теоретически для изотропных материалов может принимать значения:
Если известен коэффициент Пуассона ν, то, зная продольную деформацию, всегда можно найти поперечную деформацию:
Продольная и поперечная деформации всегда имеют разные знаки. Коэффициент Пуассона характеризует способность материала давать поперечные деформации.
Справка.
Чугун серый | ν = 0,23 ÷ 0,27 | Бетон | ν = 0,16 ÷ 0,18 |
Углеродистая сталь | ν = 0,24 ÷ 0,28 | Пробка | ν = 0,01 ≈ 0,0 |
Алюминий катанный | ν = 0,32 ÷ 0,36 | Резина | ν = 0,49 ≈ 0,05 |
