Теорема о взаимности работ внутренних сил
НАВИГАЦИЯ ПО СТРАНИЦЕ
легко понять и запомнить
Пусть к балке приложена сила , которая вызывает в сечении изгибающий момент . Приложим к балке еще и силу , которая вызвала дополнительный угол поворота сечений на участке dz равный .
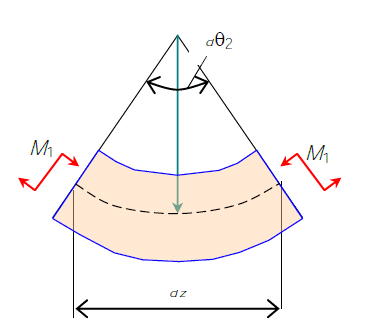
Схема деформации элементарного участка балки от действия нагрузки второго состояния
Виртуальная работа внутренних сил от на перемещениях, вызванных силой , равна:
Здесь:
Кривизна участка балки равна:
Отсюда имеем:
Получим виртуальную работу внутренних сил на элементарном участке балки:
Виртуальная работа по всей длине балки равна интегралу:
Аналогично:
Отсюда, очевидно, что:
Сформулируем теорему о взаимности работ внутренних сил:
Работа внутренних сил первого состояния на перемещениях второго состояния равна работе внутренних сил второго состояния на перемещениях первого состояния.
